judas_priest
- 174
- 0
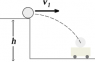
Homework Statement
What is the DISTANCE traveled by the projectile?
I know how to calculate the displacement, but this includes both x and y components, so how do I calculate the distance? I'm sure it must include both height and vertical displacement components
Homework Equations
The Attempt at a Solution
I have no clue really. Everything I try to do, it just gives me the displacement. I just don't know how to get the 'h' factor in? Do I use pythagaros? Because it doesn't apply for a curved surface.