Distributed Forces and force density....

[fog37]

TL;DR Summary

force density or pressure

Hello,
Forces can be concentrated (when acting at a single point) or distributed (when acting over a surface or line).
In the case of distributed forces, we can find the resultant concentrated force by calculating a surface or line integral of the force density $f(x)$ w.r.t. an area or length differential.

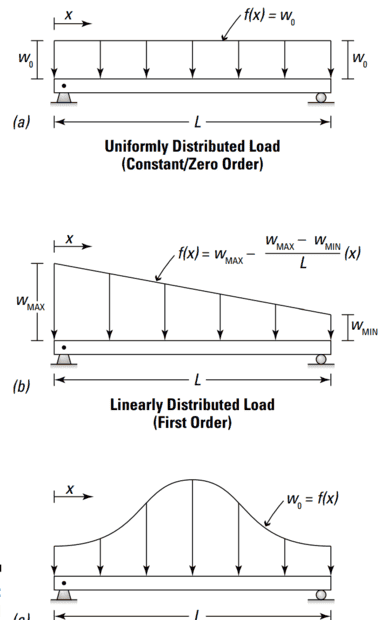
This is equivalent to adding together small products of force times infinitesimal areas. Statics books show these types of calculations. For example, $$\int \sigma dA$$
Is the force density $\sigma =f(x)$ to be considered a pressure density or a force density? Pressure is fundamentally normal force per unit area. Is $\sigma$ a pressure density only when the force direction is exactly perpendicular to the surface? The force density may be at an angle at different points on the surface with both a parallel and normal components relative to the surface.

Thanks!

 

[Dale]

Summary: force density or pressure

Is the force density σ=f(x) to be considered a pressure density or a force density?

$\sigma$ is stress, which is related to pressure but not the same thing. Stress is force density.

Pressure is the isotropic part of stress. Pressure is always normal to a surface, but in general stress can have shear components also.

 

[Lnewqban]

... Statics books show these types of calculations. For example, $$\int \sigma dA$$
Is the force density $\sigma =f(x)$ to be considered a pressure density or a force density? Pressure is fundamentally normal force per unit area. Is $\sigma$ a pressure density only when the force direction is exactly perpendicular to the surface? The force density may be at an angle at different points on the surface with both a parallel and normal components relative to the surface.

Thanks!

Sigma refers only to a normal internal force in the cross-section, which is an indirect effect of the bending load on those beams.
Please, see:
https://en.m.wikipedia.org/wiki/Bending

 

[vanhees71]

Stress is a symmetric 2nd-rank tensor. Let the components be $\sigma_{jk}=\sigma_{jk}$. It's the force per unit area acting on a surface $A$ of a continuous medium. The total force thus is
$$F_k=\int_A \mathrm{d}^2 A_j \sigma_{jk}.$$
Pressure is a special case. E.g., in an ideal fluid the stress tensor is given (in the local rest frame of the fluid) by
$$\sigma_{jk}=-P \delta_{jk},$$
where $P$ is the pressure.

It's not a force density. This would be a quantity "force per unit volume", e.g., $\vec{f}=\rho \vec{g}$ for the gravitational force close to Earth acting on a fluid.

 

[fog37]

Stress is a symmetric 2nd-rank tensor. Let the components be $\sigma_{jk}=\sigma_{jk}$. It's the force per unit area acting on a surface $A$ of a continuous medium. The total force thus is
$$F_k=\int_A \mathrm{d}^2 A_j \sigma_{jk}.$$
Pressure is a special case. E.g., in an ideal fluid the stress tensor is given (in the local rest frame of the fluid) by
$$\sigma_{jk}=-P \delta_{jk},$$
where $P$ is the pressure.

It's not a force density. This would be a quantity "force per unit volume", e.g., $\vec{f}=\rho \vec{g}$ for the gravitational force close to Earth acting on a fluid.

Thank you. So what I am calling $\sigma$ is the stress tensor (rank 2) whose integral with respect to area is the total force. So far so good. And $\sigma$ is NOT a force density. Why not? Because it is a tensor and not a vector field? The components of the stress tensor are forces either perpendicular or parallel to the surface...

In your last comment about the gravitational force you mention that $\vec{f}$ is instead a force density, force per unit volume, which I get...So the force density is a vector field, a different thing than a rank-2 tensor...Is my understanding correct? To find the overall gravitational force we calculate the volume integral of the force density $\int f dV$...

To find the overall force on a surface with calculate the surface integral of the stress tensor...

Could we have a volume integral of stress tensor? If so, what does it represent?

 

[Dale]

It's not a force density. This would be a quantity "force per unit volume"

I disagree. Current density is current per unit area. Not all densities are per unit volume. Stress is force density: force per unit area.

 

[Frabjous]

Could we have a volume integral of stress tensor? If so, what does it represent?

Yes, energy.

 

[vanhees71]

I disagree. Current density is current per unit area. Not all densities are per unit volume. Stress is force density: force per unit area.

It's again a matter of definitions. The standard nomenclature in the field-theory literature is that a density of a quantity is per volume and current density of a quantity is per unit area and unit time. In natural units with $c=1$ the dimensions are the same ;-)).

 

[Dale]

This is an engineering question, not a field-theory question.