Distribution of particles, given a function

[Omega0]

TL;DR Summary

distribution gravitation chemical reaction statistic histogram particel

I am not that super expert of statistics, so feel free to shift my formulation of the problem into the right one.First, for a physicist, the basic formulation of the problem. Let us say that you have a gravitational field and you have a fully symmetric problem on a flat world without other forces. Now let us have an emitter of particles (like an explosion) on the surface. We have a perfect symmetry, so it is okay to just take 0≤ϕ≤π2 into account, where $\phi$ is the angle from the surface of the planet to the normal.Now we take arbitrary functions into account which represent the distance which a particle can move away from the emmitting point. Probably the easiest example is if you throw away objects for perfectly random angles ϕ with a constant absolute speed v where you get the normalized solution (distance from emitting point):$$r\left( \phi \right) = \sin(2\phi)$$

Naturally, it could be something more complex like, just to stress my problem:

$$r\left( \phi \right) = \sin \left( \frac{2 \phi}{1 + 0.1 \sin(\phi)} \right)$$

but let us go for the simple problem first.My question is the following. I am happy to have the function r(ϕ) but what I really want to have is the distribution of particles over r, in the perfect case as a function. I mean I want to be able to do an integral from r1 to r2 to tell how likely it is that a particle goes there.Just for visualization please check this example:

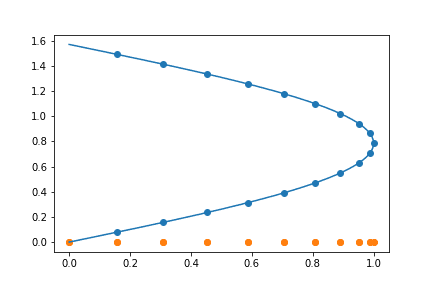
The obvious solution for this problem (correct me, if I am wrong!) is a histogram. It clearly tells me - given by numerics - the distribution over the range. Here we have the simple case sin⁡(2ϕ) where I plottet a line instead of bars. Please note that the integral here would not be perfectly correct:

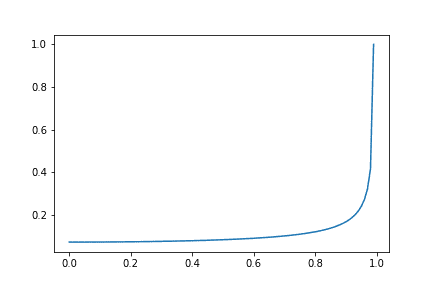Just as a note apart: This tells me why a crater looks like a crater, doesn't it? But this is not my question.My question is: How do I get a mathematical formulation for the density of the radial function f(ϕ)?Thanks!

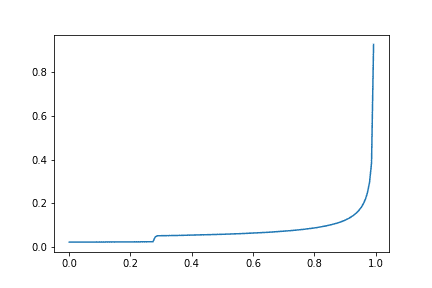
PS: I have to show you another plot, so cool, with a jump. Just to demonstrate that this is not easy to see from the original function (or is it?). I used $$r\left( \phi \right) = \sin \left( \frac{2 \phi}{1 + 0.1 \sin(\phi)} \right)$$

 

[anuttarasammyak]

Though I am not sure I understand what you stated, please find below what I thought.

It is the case for $\phi(r_1) < \phi(r_2) < \frac`{\pi}{4}$. For other cases the integral area is a little more complicated. The case you say random angle is $p(\phi)=\frac{2}{\pi}$.

 

[Omega0]

To give myself a correct reply... Here again a picture which tells everything I needed:

The blue line is the inverse "function". It is from 0 to $\pi /4$ the function but then we can take into account that it is mirrored. This means the density of particels meating the ground can simply be multiplied by 2. What we can see is that the density depends from the derivative of the inverse function $\arcsin$, so after normalization the solution is easily:

$$\rho(r) = \frac{2}{\pi}\frac{1}{\sqrt{1-r^2}}$$

I like to play around with numerics and graphics so here I just wanted to see the comparison with the linearly smoothed histogram where 2000 points have been used:

I like this little problem. I think it shows two things. The first thing is that the closed solution depends completely from the existence of the inverse function. Here we could trick around, I could mirror but this is almost always impossible. No problem, we have the histogram! It always works - altogether with other statistical tools.
The second thing I like about this example is that it shows the difference between mathematics and physics, in my eyes. For me as a physicist this picture looks a little bit like a crater after an impact but not too precise. We have so many things to take into account, for example that all the particles around $r=1$ feel gravitation and have volume, now let us assume that those particles are balls with friction etc., now we may have a way better model for the crater.
Please don't get me wrong, I am not that expert in this field of physics. I just love physics and if I am wrong in anything, just let me know!

PS: I think I will have fun the next days to calculate some crater models