Distribution of Position in classical & quantum case

[WeiShan Ng]

I am confused about the difference between the two

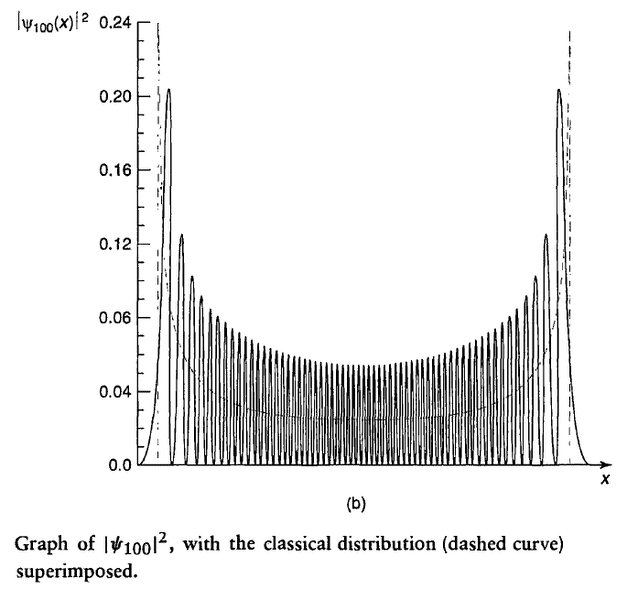
In Griffith's 2.3 The Harmonic Oscillator, he superimposes the quantum distribution and classical distribution and says

In the classical case we are talking about the distribution of positions over time for one oscillator, whereas in the quantum case we are talking about the distribution over an ensemble of identically prepared systems.

What I understand for quantum case is that $|\Psi_{100} (x)|^2$ gives the probability we will measure the particle at position $x$. So if we were given a large set of the particles we will have a probability distribution of the measured $x$ and this distribution is what shown on the graph. However I don't quite understand what the distribution over time means in the classical case. I don't really see how the dependence of time fit in, since the graph is only x-dependence.

 

[Nugatory]

However I don't quite understand what the distribution over time means in the classical case. I don't really see how the dependence of time fit in, since the graph is only x-dependence.

It is the distribution of x values that we will find if we sample the position of the one and only particle in our one and only classical oscillator repeatedly at many different times.

In the quantum mechanical case, we can't do repeated sampling on the same oscillator, so we get one sample from each of many oscillators instead of many samples from one oscillator. But either way, we end up with a large number of x values so that we can plot their distribution.