Divergence of the Electric field of a charged circular ring

[bob012345]

In a previous thread* the field in a charged ring was discussed and it was shown to be not zero except at the center. In *post #45 a video is referenced that says the field diverges as one gets close to the ring and it was argued that at very close distances the field looks like an infinite line charge which diverges so this diverges.

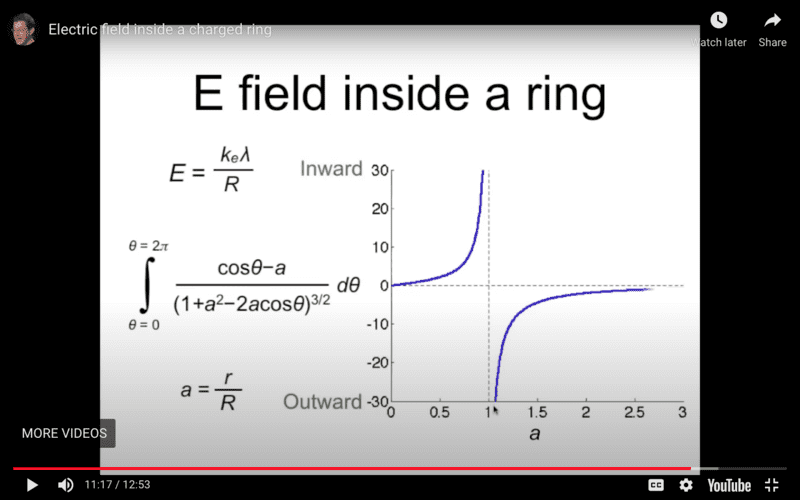
The video asserts that as $a=\frac{r}{R}→1$ the field diverges. It is based on looking at the integral and making arguments it looks like an infinite line charge as you get close but the results of the integration eliminate the divergence. It is true K(k) the complete elliptical integral of the first kind approaches infinity as k→1 but the term in front of it (1−a) approaches zero faster. This seems right and numerically works as far as I can take it which was closer than one part in $10^{−18}$ of R from the ring but I'm not sure how to prove it works in the limit or if there is a surprise where K(k) starts to grow faster and the field does diverge. The exact field is here;

$$E_r = \frac{ k_e Q}{ \pi R^2} \left[\frac{1}{a} \frac{(1-a)}{(1+a)^3} \left((1-a)K(k) - (1+a)E(k)\right)\right],~~~a>0$$

Edit: This is wrong due to an algebra mistake! There is a divergence after all and this video is correct! See below.

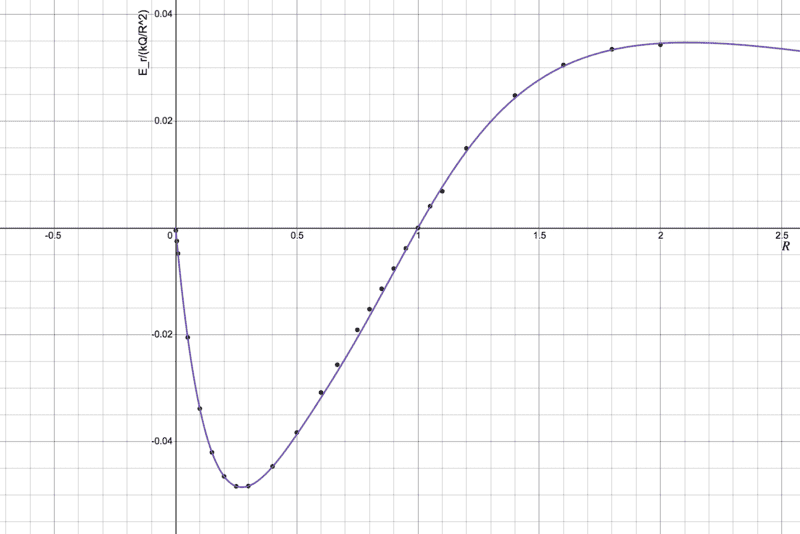
These two plots are the wrong. Corrected plot is at the bottom of the thread.
This plot shows the exact field as points and the blue curve is a series approximation based on the exact form with many terms. The black curve is a point charge of the same total charge for reference.

*https://www.physicsforums.com/threa...-point-within-a-charged-circular-ring.1006381

 

[kuruman]

Nice work. I believe it more confidently than I believe the results of the video. I have been a silent observer of the discussion in the earlier thread and, belatedly, I came up with a less daunting way to show that the field in the xy-plane for $r<a$ cannot be zero everywhere. I will provide this first because it bears some relevance to a suggestion I have for you.

The electrostatic potential obeys Laplace's equation and has axial symmetry, i.e. it can be written, in Cartesian coordinates, as $\varphi(\sqrt{x^2+y^2},z).$ Furthermore, the xy-plane is a mirror plane which means that the potential is an even function, $\varphi(\vec r)=\varphi(-\vec r)$.

It follows that if we expand the potential about the center of the ring, the odd terms are zero. The zeroth term is obviously $\varphi(0,0,0)=\frac{kQ}{R}$. The next term is the second-order (quadrupole) term, $$\frac{1}{2}\sum_{i=1}^3V_{ii}x_i^2 ~;~~V_{ii}=\left. \frac{\partial^2 \varphi}{\partial x_i^2}\right |_{\vec r=0}.$$ Because of the axial symmetry, $V_{xx}=V_{yy}$. Furthemore, because Laplace's equation is valid at the origin, $$V_{xx}+V_{yy}+V_{zz}=0\implies V_{xx}=V_{yy}=-\frac{1}{2}V_{zz}.$$ We can get $V_{zz}$ from the potential on the z-axis, $$\varphi(0,0,z)=\frac{kQ}{(z^2+R^2)^{1/2}}\implies V_{zz}=\left. \frac{\partial^2 \varphi(0,0,z)}{\partial z^2}\right |_{z=0}=-\frac{kQ}{R^3}.$$We can now write the potential in a region near the origin as $$\varphi(x,y,z)=\frac{kQ}{R}+\frac{1}{2}\frac{kQ}{R^3}\left[\frac{1}{2}(x^2+y^2)-z^2\right]=\frac{kQ}{R}+\frac{kQ}{4R^3}\left(\rho^2-2z^2\right), ~~~\rho=\sqrt{x^2+y^2}.$$From this we find the components of the electric field near the origin, $$E_{\rho}=-\frac{\partial \varphi}{\partial\rho}=-\frac{kQ}{2R^3}\rho~;~~E_{z}=-\frac{\partial \varphi}{\partial z}=\frac{kQ}{R^3}z.$$Clearly, in the plane of the ring and in the vicinity of the origin, the electric field has a negative radial component. The figure below shows the vector field near the origin.

We can construct a Gaussian pillbox (gray rectangle) enclosing the origin and calculate the total flux through it; it should be zero. The flat faces are at $\pm z$ and they have radius $\rho$. $$\Phi_{\text{side}}=(2\pi \rho \times 2z)E_{\rho}=(2\pi \rho\times 2z)E_{\rho}=-(2\pi \rho\times 2z)\frac{kQ}{2R^3}\rho=-\frac{2kQ\pi \rho^2 z}{R^3}.$$ $$\Phi_{\text{top}}+\Phi_{\text{bottom}}=2\times \pi \rho^2 E_{z}=2\pi \rho^2\frac{kQ}{R^3}z.$$Clearly the net flux through the Gaussian pillbox is zero, Gauss's law is verified and life is good.

Why am I mentioning all this? To begin with, you now have an expression for $\frac{\partial E_{\rho}}{\partial \rho}$ near the origin that does not involve pesky elliptic integrals and provides a fixed parameter in your polynomial expansion. BTW, I hope that you have limited your series approximation to odd terms only because the potential is even therefore the electric field must be an odd function.

Have you considered finding the potential and hence the electric field at $z \neq 0$? I have some tentative ideas about that which I could discuss with you. Send me a PM if interested.

 

[anuttarasammyak]

I observe electric potential is
$$\phi=\frac{k_e\lambda}{1-a}\int_0^{2\pi}\frac{d\theta}{\sqrt{1+b \sin^2{\frac{\theta}{2}}}}$$
where
$$b=\frac{4a}{(1-a)^2}$$
I observe no singularity.

 

[bob012345]

Nice work. I believe it more confidently than I believe the results of the video. I have been a silent observer of the discussion in the earlier thread and, belatedly, I came up with a less daunting way to show that the field in the xy-plane for $r<a$ cannot be zero everywhere. I will provide this first because it bears some relevance to a suggestion I have for you.

Thanks. I will study your solution.

Why am I mentioning all this? To begin with, you now have an expression for $\frac{\partial E_{\rho}}{\partial \rho}$ near the origin that does not involve pesky elliptic integrals and provides a fixed parameter in your polynomial expansion. BTW, I hope that you have limited your series approximation to odd terms only because the potential is even therefore the electric field must be an odd function.

I used the series expansion of the actual complete elliptical integrals;

$$ K(k) =\frac{\pi}{2} \sum_{n=0}^{∞}\left(\frac{\left(2n\right)!}{\left(2^{\left(2n\right)}\right)\left(n!\right)^{2}}\right)^{2}\ \ k^{2n}$$

$$E(k) = \frac{\pi}{2} \sum_{n=0}^{∞}\left(\frac{\left(2n\right)!}{\left(2^{\left(2n\right)}\right)\left(n!\right)^{2}}\right)^{2}\ \ \left(\frac{-1}{2n-1}\right)k^{2n}$$

Have you considered finding the potential and hence the electric field at $z \neq 0$? I have some tentative ideas about that which I could discuss with you. Send me a PM if interested.

OK, I'd like to hear.

 

[bob012345]

I observe electric potential is
$$\phi=\frac{k_e\lambda}{1-a}\int_0^{2\pi}\frac{d\theta}{\sqrt{1+b \sin^2{\frac{\theta}{2}}}}$$
where
$$b=\frac{4a}{(1-a)^2}$$
I observe no singularity.

How did you arrive at this? Is $a =\large \frac{r}{R}$?

 

[bob012345]

From this we find the components of the electric field near the origin, $$E_{\rho}=-\frac{\partial \varphi}{\partial\rho}=-\frac{kQ}{2R^3}\rho~;~~E_{z}=-\frac{\partial \varphi}{\partial z}=\frac{kQ}{R^3}z.$$Clearly, in the plane of the ring and in the vicinity of the origin, the electric field has a negative radial component. The figure below shows the vector field near the origin.

I can confirm the field near zero is what you say with this blowup of the plot; The slope is $-\frac{1}{2}$.

 

[anuttarasammyak]

How did you arrive at this? Is a=rR?

Yes, a is r/R following the video you refer.

We can make use of the fact that the distance from the point r to the element of ring is
$$\sqrt{R^2+r^2-2Rr\cos\theta}$$

 

[bob012345]

Yes, a is r/R following the video you refer.

We can make use of the fact that the distance from the point r to the element of ring is
$$\sqrt{R^2+r^2-2Rr\cos\theta}$$

What about the $1 - a$ term in your denominator? Isn't that a singularity as $a→1$?

 

[anuttarasammyak]

Ah, yes. Now I got your problem. Thank you.

Let us think it in 3D not on xy plane but in xyz space. Formula (1) in the attached sketch shows potential. Fig.1 shows that for small but not zero z it does not diverge. Fig.2 shows cross section S in 3D world ring. Fig. 3 shows a case that a ring consists of two rings one is above xy plane and the other is below it. Though it is arranged with an intention, we can avoid divergence. We may say divergent or not depends on details of cross section of ring.

 

[anuttarasammyak]

Potential diverges or not seems to depend on there is charge or not on the point of measurement. If the ring consists of assemble of finite point charges, there may or not be charge on the point of measurement. If charge is continuous like fluid, there is infinitely less charge on the point of measure so potential would not diverge or the degree of divergence would be weakened at least.

 

[bob012345]

It turns out I was quite wrong about the lack of divergence of the field at $a = 1$. Thanks to @kuruman for helping me to see my error. There is a divergence and the video was correct. I had made an algebra mistake while simplifying the expression for the field. The correct field looks like this;

$$E_r = \frac{ k_e Q}{ \pi R^2} \left[ \frac{1}{a} \left(\frac {K(k)}{(1+a)} - \frac{E(k)}{(1-a)}\right)\right],~~~a>0$$

The plot looks like this $(a=\frac{r}{R})$; The black curve is a point charge of equivalent total charge for reference.

 

[rude man]

Not sure if I'm contributing but the fact is that there is no divergence of the E field inside the ring:
$\nabla \times \bf D = \rho$
No charge inside the ring, no divergence of E.

 

[vanhees71]

It must be $\vec{\nabla} \cdot \vec{D}=\rho$ of course.