Lambda96
- 233
- 77
- Homework Statement
- Calculate the following ##\vec{\nabla}\cdot \vec{E}(\vec{r})##
- Relevant Equations
- none
Hi,
unfortunately, I am not sure if I have calculated the task correctly
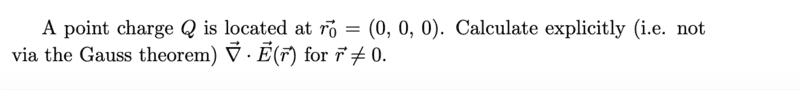
The electric field of a point charge looks like this ##\vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0}\frac{\vec{r}}{|\vec{r}|^3}## I have now simply divided the electric field into its components i.e. #E_x , E-y, E_z#.
$$\vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0}\left( \begin{array}{rrr}
\frac{x}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\frac{y}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\frac{z}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\end{array}\right)$$
Then I calculated the divergence
$$\vec{\nabla}\cdot \vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0} \Bigl( \frac{\partial}{\partial x}\frac{x}{(x^2+y^2+z^2)^{\frac{3}{2} }} +\frac{\partial}{\partial y}\frac{y}{(x^2+y^2+z^2)^{\frac{3}{2} }} +\frac{\partial}{\partial z}\frac{z}{(x^2+y^2+z^2)^{\frac{3}{2} }} \Bigr)=\Bigl( \frac{-2x^2+y^2+z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} +\frac{x^2-2y^2+z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} +\frac{x^2+y^2-2z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} \Bigr)=0$$
With the result of 0 I am a bit confused, in the task is not mentioned the sign of the charge, but with a positive charge I would expect as a divergence a source, so the divergence would have to be positive and with a negative charge, a sink, so a negative divergence.
Have I somehow miscalculated, or do I have a thinking error in the physical interpretation of the result?
unfortunately, I am not sure if I have calculated the task correctly
The electric field of a point charge looks like this ##\vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0}\frac{\vec{r}}{|\vec{r}|^3}## I have now simply divided the electric field into its components i.e. #E_x , E-y, E_z#.
$$\vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0}\left( \begin{array}{rrr}
\frac{x}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\frac{y}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\frac{z}{(x^2+y^2+z^3)^{\frac{3}{2}}} \\
\end{array}\right)$$
Then I calculated the divergence
$$\vec{\nabla}\cdot \vec{E}(\vec{r})=\frac{Q}{4 \pi \epsilon_0} \Bigl( \frac{\partial}{\partial x}\frac{x}{(x^2+y^2+z^2)^{\frac{3}{2} }} +\frac{\partial}{\partial y}\frac{y}{(x^2+y^2+z^2)^{\frac{3}{2} }} +\frac{\partial}{\partial z}\frac{z}{(x^2+y^2+z^2)^{\frac{3}{2} }} \Bigr)=\Bigl( \frac{-2x^2+y^2+z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} +\frac{x^2-2y^2+z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} +\frac{x^2+y^2-2z^2}{(x^2+y^2+z^2)^{\frac{5}{2} }} \Bigr)=0$$
With the result of 0 I am a bit confused, in the task is not mentioned the sign of the charge, but with a positive charge I would expect as a divergence a source, so the divergence would have to be positive and with a negative charge, a sink, so a negative divergence.
Have I somehow miscalculated, or do I have a thinking error in the physical interpretation of the result?