- #1
FluidStu
- 26
- 3
The Navier-Stokes equation is:
(DUj/Dt) = v [(∂2Ui/∂xj∂xi) + (∂2Uj/∂xi∂xi)] – 1/ρ (∇p)
where D/Dt is the material (substantial) derivative, v is the kinematic viscosity and ∇p is the modified pressure gradient (taking into account gravity and pressure). Note that the velocity field is non-solenoidal (∇⋅U ≠ 0).
How, then, can we take the divergence of this equation and get the following result?:
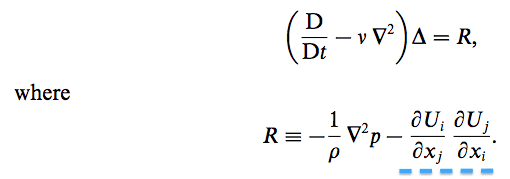
I can follow all of the terms other than the one underlined in blue. I know that it comes from the blue section of the Navier-Stokes written above, since I can easily get all the other terms.
Thanks in advance
(DUj/Dt) = v [(∂2Ui/∂xj∂xi) + (∂2Uj/∂xi∂xi)] – 1/ρ (∇p)
where D/Dt is the material (substantial) derivative, v is the kinematic viscosity and ∇p is the modified pressure gradient (taking into account gravity and pressure). Note that the velocity field is non-solenoidal (∇⋅U ≠ 0).
How, then, can we take the divergence of this equation and get the following result?:
I can follow all of the terms other than the one underlined in blue. I know that it comes from the blue section of the Navier-Stokes written above, since I can easily get all the other terms.
Thanks in advance