- #1
mattg443
- 12
- 0
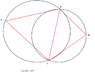
I was wondering if the common chord of two intersecting circles subtends an equal angle in both circles at the circumference (in no special cases i.e different radii circles etc)
If not, are there any special case(s) where this would work, making these two triangles similar or ABDC is a kite/special quadrilateral...
(see diagram please)
Thanks!
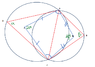
If not, are there any special case(s) where this would work, making these two triangles similar or ABDC is a kite/special quadrilateral...
(see diagram please)
Thanks!