Do we calculate the integral in that way?

[mathmari]

Hey!

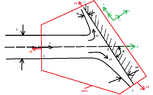
A two-dimensional fluid stream of thickness $S$ and velocity $c$ (evenly distributed through the thickness of the stream) falls on a stationary plate and gets separated. Calculate the ratio of thicknesses $\frac{S_1}{S_2}$ as a function of the angle $\phi$.

View attachment 4421In my notes there is this solution:

Continuity equation:

Let $c_1$, $c_2$ the velocities of the sections 1, 2

$$0: \overrightarrow{u}=c\hat{e} \ \ , \ \ \overrightarrow{n}_0=-\hat{e}=-(-\sin \phi \hat{i}+\cos \phi \hat{j}) \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_0=-c \\ 1: \overrightarrow{u}=c_1 \overrightarrow{n}_1=c_1 \hat{i} \ \ , \ \ \overrightarrow{n}_1=\hat{i} \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_1=c_1 \\ 2: \overrightarrow{u}=c_2 \overrightarrow{n}_2=-c_2\hat{i} \ \ , \ \ \overrightarrow{n}_2=-\hat{i} \Rightarrow \overrightarrow{u} \cdot \overrightarrow{n}_2=c_2$$

$$\int_{\partial{W_1}}\overrightarrow{u} \cdot \overrightarrow{n}dA=0 \Rightarrow -c \cdot (S \cdot 1)+c_1 \cdot (S_1 \cdot 1)+c_2 \cdot (S_2 \cdot 1)=0 \Rightarrow cS=c_1S+c_2S_2 \ \ \ \ \ (1) $$

Conservation of energy $\Rightarrow $ Bernoulli equation

$$\frac{1}{2}|\overrightarrow{u}|^2+\frac{p}{\rho_ 0}=\text{ constant along a streamline }$$

$$0 \rightarrow 1 : \frac{1}{2}c^2+\frac{p_a}{\\rho_0}=\frac{1}{2}c_1^ 2+\frac{p_a}{\rho_0} \Rightarrow c_1=c \\ 0 \rightarrow 2 : \frac{1}{2}c^2+\frac{p_a}{\\rho_0}=\frac{1}{2}c_2^ 2+\frac{p_a}{\rho_0} \Rightarrow c_2=c \\ \Rightarrow c_1=c_2=c \ \ \ \ \ (2)$$

$$(1) \wedge (2) \Rightarrow S=S_1+S_2 \ \ \ \ \ (3)$$

$$\overrightarrow{F}_{W_0}=-\int_{\partial_{W_1}}p \overrightarrow{n} dA-\int_{\partial{W_1}}\rho \overrightarrow{u} (\overrightarrow{u} \cdot \overrightarrow{n})dA$$

$$\int_{\partial_{W_1}}p \overrightarrow{n} dA=p_a \int_{\partial{W_1}}\overrightarrow{n}dA=0$$

$$\int_{\partial{W_1}}\rho \overrightarrow{u} (\overrightarrow{u} \cdot \overrightarrow{n})dA=\rho_0 (c \hat{e}(-c)S+c_1 \hat{i}c_1S_1+(-c_2 \hat{i})c_2S_2)=(\rho_0c^2S\cos \phi +\rho_0 c_1^2S_1-\rho_0c_2^2S_2)\hat{i}-\rho c^2S\sin \phi \hat{j}=-\overrightarrow{F}_{W_0}$$

$$F_{W_0, x}=-\rho_0c^2(S\cos \phi +S_1-S_2) \ \ \ \ \ (4a) \\ F_{W_0, y}=\rho c^2 S \sin \phi \ \ \ \ \ (4b)$$

Since the fluid is ideal we have that $$F_{W_0, x}=0 \Rightarrow S_2-S_1=S \cos \phi \ \ \ \ \ (5)$$

$$(3) \wedge (5) \Rightarrow \\S_1=\frac{S}{2}(1+\cos \phi) \\ S_2=\frac{S}{2}(1-\cos \phi) \\ \Rightarrow \frac{S_2}{S_1}=\frac{1-\cos \phi}{1+\cos \phi}$$
Do we calculate the integral $$\int_{\partial{W_1}}\overrightarrow{u} \cdot \overrightarrow{n}dA=0 \Rightarrow -c \cdot (S \cdot 1)+c_1 \cdot (S_1 \cdot 1)+c_2 \cdot (S_2 \cdot 1)=0$$ as followed?

$$\int_{\partial{W_1}}\overrightarrow{u} \cdot \overrightarrow{n}dA=0 \Rightarrow \int_{(0)} \overrightarrow{u} \cdot \overrightarrow{n}dA+\int_{(1)}\overrightarrow{u} \cdot \overrightarrow{n}dA+\int_{(2)}\overrightarrow{u} \cdot \overrightarrow{n}dA=0 \Rightarrow -c\int_{(0)} dA+c_1 \int_{(1)}dA+c_2 \int_{(2)}dA=0$$

To find the integral $\int_{(0)} dA$ do we take a part of the section $(0)$ and calculate its area?? (Wondering)

 

[jvicens]

Hello! Yes, the integral $\int_{(0)} dA$ can be found by taking a part of the section $(0)$ and calculating its area. The continuity equation is used to ensure that the fluid flow is balanced and the Bernoulli equation is used to calculate the velocities at each section. The force on the plate is then calculated using the pressure and velocity terms. I hope this helps!