Callmelucky
- 144
- 30
- Homework Statement
- Do we always need to exclude solutions that would give 0 in the denominator of a fraction?
- Relevant Equations
- 1/x
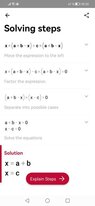
When working with fractions and when we have a fraction or equation with fractions like this one for example ##\frac{x}{x-1}+\frac{x}{x+1}=\frac{9}{4}## do we always need to set boundaries? Like, do we always need to write that x can't be a number that would give the denominator 0? In this particular case x can't be 1 and -1. Because that would equal 0 and we can't have 0 in the denominator.
I know it's kind of a stupid question and the answer is kind of obvious but I am not sure if that should be stated in the problem by the author or if I am supposed to do that.
Thank you.
I know it's kind of a stupid question and the answer is kind of obvious but I am not sure if that should be stated in the problem by the author or if I am supposed to do that.
Thank you.
Last edited: