Daniel Petka
- 147
- 16
- TL;DR
- I'm wondering if it is possible to measure the discrete charging steps for the step response of a FP cavity with an oscilloscope.
I'm trying to understand the Fabry Perot interferometer and came across this amazing video.

Basically it all comes down to adding E-fields together with each of them being delayed by the cavity round trip time. In the extreme case, either they all interfere constructively at the second mirror and the transmission goes to 100% if the length is an even multiple of half-wavelength and close to 0% if it's an odd multiple according to the airy formula.
Now I'm wondering how the FP could react to a step response of coherent CW laser light. In my EM class we did a step response for transmission lines. The result is similar to the charging of a capacitor but it's discrete because the wave takes some time to come back and interfere (round trip time)
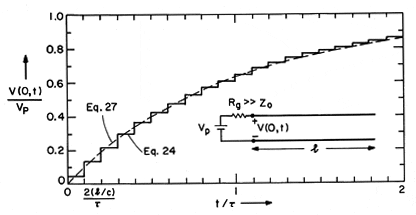
Would it look the same for a FP? And if yes, is this something that can be measured with an oscilloscope? For a 1m cavity, the steps should be 1/c seconds long, so approx. 3.3 ns, this shouldn't be a problem but I haven't seen anyone measure it...
I came across this paper called "Rapid-Swept CW Cavity Ring-down Laser Spectroscopy for Carbon Isotope Analysis"

Here they seem to ignore all the discrete summation and just approximate the solution as a decaying exponential. I've seen the exponential various times without addressing the individual charging steps. Is there a flaw in my model? Thanks!
Basically it all comes down to adding E-fields together with each of them being delayed by the cavity round trip time. In the extreme case, either they all interfere constructively at the second mirror and the transmission goes to 100% if the length is an even multiple of half-wavelength and close to 0% if it's an odd multiple according to the airy formula.
Now I'm wondering how the FP could react to a step response of coherent CW laser light. In my EM class we did a step response for transmission lines. The result is similar to the charging of a capacitor but it's discrete because the wave takes some time to come back and interfere (round trip time)
Would it look the same for a FP? And if yes, is this something that can be measured with an oscilloscope? For a 1m cavity, the steps should be 1/c seconds long, so approx. 3.3 ns, this shouldn't be a problem but I haven't seen anyone measure it...
I came across this paper called "Rapid-Swept CW Cavity Ring-down Laser Spectroscopy for Carbon Isotope Analysis"
Here they seem to ignore all the discrete summation and just approximate the solution as a decaying exponential. I've seen the exponential various times without addressing the individual charging steps. Is there a flaw in my model? Thanks!