PainterGuy
- 938
- 73
Hi,
Let's call the box in green a plant. Does every plant consist of an integrator? It has to because when \overset{\cdot }{x}(t) passes through the green box, it becomes x(t). It's an operation of integrator; integrator converts the derivative back to the variable. Could you please guide me?
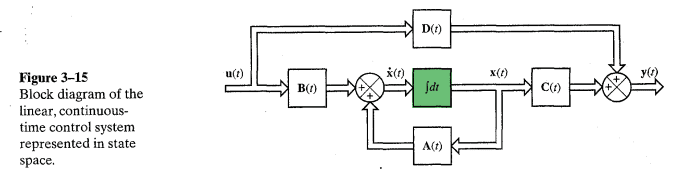
Let's call the box in green a plant. Does every plant consist of an integrator? It has to because when \overset{\cdot }{x}(t) passes through the green box, it becomes x(t). It's an operation of integrator; integrator converts the derivative back to the variable. Could you please guide me?