buchi
- 8
- 0
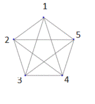
how would one possibly draw all the possible Eulerian circuits? the way I am thinking of it is if we start say at vertex 1 and go through each vertex and edge and come back to vertex 1 then we can do the same for each vertex up to 5 but then we can also start at vertex one and head a different way to arrive at the same vertex so I guess my question is is there a systematic way to calculate how many different paths we could take? and to draw them? would we just draw exactly the same picture however many times and putting an arrow showing the path?
Thanks
Thanks