Does Ohm's Law work for Light Bulbs?

[Albertgauss]

TL;DR Summary

Does Ohm's Law work for Light Bulbs? I did a simple experiment where it doesn't seem to.

Does Ohm’s Law, V = IR work for light bulbs? It appears not to from my simple experiment below.

In the figure below, I measured the resistance of a lightbulb and found that resistance to be 2.6 ohms.

However, when I connect this lightbulb into the circuit where I measure the voltage across the lightbulb and the current through the lightbulb simultaneously, the entire simple circuit sourced by a power supply, then I get a derived resistance of 18 ohms.

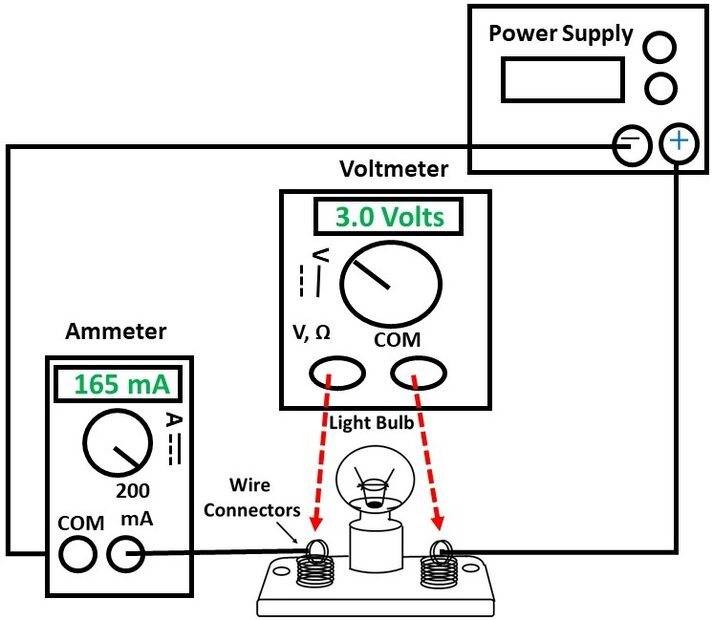
I say derived because the voltage I measure is 3 Volts across the lightbulb and the current through the lightbulb is 165 mA. By Ohm’s law, 3 Volts divided by 165 mA is equal to 18 ohms. If the resistance of the lightbulb with current flowing through it is indeed 18 ohms, this certainly does not match the resistance of 2.6 Ohms measured directly by the resistance meter of the multimeter. From such an experiment, I would conclude the Ohm’s law does not work for light bulb.

Can anyone confirm that Ohm’s law does not work for a light bulb?

Obviously, the lightbulb heats up, and that heat could change the resistance dramatically when the lightbulb has current flowing through it versus when there is no current flowing; this is the only explanation I can think of off the top of my head of why Ohm’s law does not work for a lightbulb.

I actually measured the resistance of all the wires, the ammeter, etc and their total resistances still came to around 3 ohms; thus, the high resistance of 18 Ohms measured by the lightbulb when On cannot be attributed to the resistances of other components in the circuit.

 

[TSny]

Obviously, the lightbulb heats up, and that heat could change the resistance dramatically when the lightbulb has current flowing through it versus when there is no current flowing; this is the only explanation I can think of off the top of my head of why Ohm’s law does not work for a lightbulb.

Yes, that's correct.

See these comments.

 

[DaveE]

Ohm's law does not work for a light bulb. It does behave like a resistor, but the value of its resistance is a strong function of the filament temperature. Its resistance increases dramatically as it heats up.

 

[DaveE]

BTW, Ohm's Law isn't really a law like conservation of momentum. It should have been called Ohm's Approximation. It is very useful, and is a good approximation for a lot of resistive materials. But it just isn't true for other things like incandescent lamps, semiconductors, and other stuff.

 

[phinds]

Ohm's law does not work for a light bulb.

That's not exactly true. At every instant of time, Ohms Law DOES apply --- it's just that a light bulb is not a simple resistor so you can't measure current at one time and voltage at another and get a meaningful value for resistance (until/unless it has reached steady state).

 

[russ_watters]

BTW, Ohm's Law isn't really a law like conservation of momentum. It should have been called Ohm's Approximation. It is very useful, and is a good approximation for a lot of resistive materials. But it just isn't true for other things like incandescent lamps, semiconductors, and other stuff.

I'm having a real difficulty with that take. Even the OP uses Ohm's Law to "disprove" Ohm's law. Yes, the resistance changes with temperature. How do you track that change? With Ohm's law. Ohm's law is true for a single-point situation/measurement and does not imply consistency over time and between different circumstances/scenarios. It works when the light bulb is on and it works when the light bulb is off. Just don't confuse them for two parts of the same scenario.

We get exactly the same misuse asked about for Bernoulli's equation. People change the setup and then try to apply Bernoulli's to two different scenarios at the same time.

[edit] Beaten by @phinds

 

[anorlunda]

BTW, Ohm's Law isn't really a law like conservation of momentum. It should have been called Ohm's Approximation.

I think that's a very good way of stating it. It is just a lucky accident that Ohm's Law works even approximately over any region.

I like to remind myself with a plot of the voltage-current characteristic of a solar PV cell. The slope of that curve at any point $\frac{\partial V}{\partial I}$ is the resistance, but the slope is hardly constant, nor is the intercept (0,0). However, there are regions where the curve approximates a straight line (constant resistance), so that the Thevanin's equivalent resistance would be constant.

 

[berkeman]

Thread closed temporarily for Moderation. Lordy...

 

[berkeman]

That's not exactly true. At every instant of time, Ohms Law DOES apply

Correct, yes it does. To say otherwise is to ignore the physics of the situation. And we don't allow that at PF.

If folks want to point out that approximations (like assuming constant temperature or constant density or real impedance instead of complex impedance) seem to give wrong results, that's okay as long as they acknowledge the approximation. But please don't say stuff like "Ohm's law is wrong" or that it doesn't apply to some situations.

Thread is reopened for now...

https://en.wikipedia.org/wiki/Ohm's_law

 

[malawi_glenn]

But please don't say stuff like "Ohm's law is wrong" or that it doesn't apply to some situations.

Is there a source where the absolute and true definition of Ohms law are to be read about?
Like when you play scrabble, you agree upon a dictionary to use if someone makes a combination of letters that actually is not a word according to that dictionary.

 

[berkeman]

I added the Wikipedia link to my post. It's got a good discussion about it and also related / similar laws (like heat conduction).

 

[DaveE]

I think the key thing in this thread is the framing in the OP. It's an excellent post that includes his test setup: a lamp, DC power supply, voltmeter, and ammeter. This is an experiment to collect the (stable) DC operating point data. That data will produce a non-linear curve that does not follow ohm's law. Even in a small region, the slope of that curve, when extrapolated, will not cross through the origin (V=0, I=0), which is required by Ohm's Law. The local electrical model for the DC bias curve would be a DC voltage source in series with a resistor.

However, if he had a signal generator, and a network or frequency response analyzer, the context would be different. For AC excitation that is fast enough to not disturb the DC equilibrium. This lamp does behave like a resistor (as I originally said). It's value is not the slope of the non-linear DC curve, it's essentially the value obtained from a line through the origin and the DC bias point, so Ohm's law does apply in this small signal context.

However, there are materials (usually composites) that simply do not follow Ohm's law: diodes, MOVs, gas discharge tubes, some polymers, etc. So, yes, Ohm's Law works, but only for resistors, which is a circular definition, IMO; a tautology. Although any real world function can be well approximated by a 1st order Taylor's series if you have a small signal. Then if you can ignore the constant term, it's a resistor.

He asked a simple question and in that context we confirmed his assessment. Then (common at PF) we all spun it up to a complex discussion of things he didn't ask about.

 

[JT Smith]

It seems like a picky question of definition of the law. What is it exactly? Wikipedia doesn't clear up the question entirely. It mentions non-ohmic materials and on first glance this example seems to fall into that category. But at a low enough current or with sufficient cooling provided then the change in resistance wouldn't be observed.

So what does it mean? It's a very useful relationship but it doesn't work over all conditions. One can generalize to simply mean the ratio of current to voltage at a given point in time but that's not really a "law".

 

[hutchphd]

I find myself staring at the screen and scratching my head. My understanding of Ohm's Law, divorced from any historical context, is the following:

1. For a two-port device we define its resistence R for DC (direct current) $$R=\frac V I$$
2. Ohm's Law states that to a useful approximation R does not depend directly upon I for many circuit elements.

The result is surprising and contains lots of physics, but is this not the generic understanding? What subtlety am I failing to grasp here?

/

 

[Vanadium 50]

I find myself staring at the screen and scratching my head. My understanding of Ohm's Law, divorced from any historical context, is the following:

1. For a two-port device we define its resistence R for DC (direct current) $$R=\frac V I$$
2. Ohm's Law states that to a useful approximation R does not depend directly upon I for many circuit elements.

The result is surprising and contains lots of physics, but is this not the generic understanding? What subtlety am I failing to grasp here?

I would say Ohm's law defines resistance. An good (ideal) resistor is one whose resistance is approximately (exactly) independent of applied voltage over its range of operating voltages. Light bulbs are far from ideal resistors.

 

[DaveE]

I find myself staring at the screen and scratching my head. My understanding of Ohm's Law, divorced from any historical context, is the following:

1. For a two-port device we define its resistence R for DC (direct current) $$R=\frac V I$$
2. Ohm's Law states that to a useful approximation R does not depend directly upon I for many circuit elements.

The result is surprising and contains lots of physics, but is this not the generic understanding? What subtlety am I failing to grasp here?

/

Yes that's a good definition. However, in general, we might have devices (materials) that have a more complex relationship between voltage and current. For a real function V(I) you can express it as a Taylor's series. Ohm's Law says only the second term is important ($V(I) = \frac{\partial V}{\partial I} ⋅ I \equiv r ⋅ I$). Usually he's right.

PS: Even for non-linear stuff, I wouldn't complain if you were to talk about its resistance. We would just assume you meant the first derivative. This is common for things like batteries or zener diodes, even though they don't follow Ohm's Law.

 

[bob012345]

For anyone interested, here is the human side of Ohm's law. A short biography of Georg Ohm;

https://mathshistory.st-andrews.ac.uk/Biographies/Ohm/

 

[anorlunda]

Even with nonlinear devices, one can always do piecewise linear and use $R=\frac{\partial V}{\partial I}$. No matter what the topology of the circuit, circuit analysis methods can be used to solve that linearized piece.

Think of Maxwell's Equations, that can also be stated in integral and differential forms. The differential form of R is not useless, it is just unfamiliar to most of us.

Think of the continental power grid as a circuit. Nearly every load connected to the grid is nonlinear. How do we handle it? We declare the (approximately) linear portions of the grid to be the circuit to solve with circuit analysis and Ohm's Law, and those nonlinear loads as boundary conditions. It's just an analysis trick to solve problems that might otherwise be too difficult.

 

[JT Smith]

Even with nonlinear devices, one can always do piecewise linear and use $R=\frac{\partial V}{\partial I}$. No matter what the topology of the circuit, circuit analysis methods can be used to solve that linearized piece.

How does that work with a light bulb where the resistance is really a function of temperature?

 

[berkeman]

How does that work with a light bulb where the resistance is really a function of temperature?

What do you mean? Who cares if the resistance is a function of temperature and changes with time?
$$ V(t) = I(t) ~ R(t) $$

 

[russ_watters]

Regarding variation with temperature, a thermistor is a resistor with a high temperature dependence. You hold the voltage constant, measure the amperage and use Ohm's Law to calculate the resistance, which is thus a proxy for temperature:
https://en.wikipedia.org/wiki/Thermistor

 

[hutchphd]

So Ohm's law is simply a statement that the ratio of voltage to current is an interesting and useful parameter. Or, if you prefer the "dynamic resistance", for some proscribed $$\frac {\Delta V} {\Delta I}$$ is locally useful and we'll call it R.
Seems OK to me I guess...in a Peggy Lee sort of way

 

[malawi_glenn]

This is basically how I present resistance and Ohms law in my class

1) Resistance is defined as the ratio of voltage drop V and current I

2) for certain electrical components, there is a linear relationship between V and I, at least for a range of V and I. Such components are called "Ohmic". Then I show this for a resistor. The linear relation is "perfect" and we assign a resistance for the entire resistor

3) Then I show voltage and current for a light bulb, at first the relation is linear (at least to naked eye) but the more the voltage is increased, the current is no longer following a linear relationship. We call the light bulb "non-ohmic". We can still talk about resistance of the light bulb according to Ohms law, but we have to do that for a certain voltage.

4) Back to the resistor, I crank up the voltage so that the resistor gets really hot (you can smell a little burnt don't you) and the linear relationship is "destroyed"

 

[vanhees71]

From another point of view the resistance is related to electric conductivity, and as any transport coefficient it's dependent on temperature.

 

[hutchphd]

And to be fair to Ohm historically I believe he was concerned with the transport aspect and the interplay with geometrical shape effects on resistance

 

[anorlunda]

I forgot to mention the complex AC case.

$\bar Z=\frac{\bar V}{\bar I}$

Where Z is the complex impedance which could have R, L and C components. V and I are also complex.

Is that not Ohm's Law also?

Also, elaborating on @berkeman's point, V and I and Z could be functions of time and temperature, and perhaps other things too. So the equations become even more difficult to solve. Yet inherent in the equations are relationships between V and I that we call Ohm's Law, (and Kirchhoff's Laws also.)

The misunderstanding IMO is that the simplest case of Ohm's Law $R=\frac{V}{I}$ where R, V, and I are all constant in time and independent of other variables, is the one and only expression of Ohm's Law.

 

[erobz]

I'm confused. Is Ohm's Law a "Law", or "Rule". I see people saying it's a "rule" and moderation saying its a "law, and we can't say otherwise"?

Is Newtons Law even a "Law". It has a finite range of applicability too?

What is given the status of a "law", something that has not been experimentally falsified to date? If I were a betting man, I'd say that all of our "laws" are domed to become "rules" at some point in time.

 

[Jodo]

We need a good insight article on this.
I have been taught it's a law from the early 80's onward.

 

[JT Smith]

It's a law in the case where the resistance is constant. But in the general case where it's non-linear or where the voltage isn't even a function of only the current then it's just a definition, the ratio of the voltage and current. With a thermistor you can at least say that the resistance is constant for a given temperature. But for a light bulb predicting the current is more complicated.

I think Ohm's Law would never have been conceived if there were no materials that behaved in an "ohmic" fashion.

 

[anorlunda]

Words like law, rule, theory are accidents of history. Why Newton's Laws, but Einstein's Theory of Relativity? Quantum Mechanics is not referred to as a law or a rule or a theory, it's just Quantum Mechanics. There are no language police to enforce uniform definitions of which word to use in which cases.

By the way, back in 2016 I wrote an Insights Article (with help from the late Jim Hardy), Learn Why Ohm’s Law Is Not a Law.

 

[malawi_glenn]

By the way, back in 2016 I wrote an Insights Article (with help from the late Jim Hardy), Learn Why Ohm’s Law Is Not a Law.

No idea why that link did not work for me, but I found it here
https://www.physicsforums.com/insights/ohms-law-mellow/

 

[vanhees71]

Well, Ohm's Law indeed can be derived. Historically the first was Drude's theory, which has been refined quantum-mechanically by Sommerfeld. It's one of the first applications of quantum statistics in condensed-matter physics.

 

[anorlunda]

That derivation can be found here:
https://en.wikipedia.org/wiki/Drude_model#DC_field
It's also discussed in that Insights article.

@vanhees71 has spoken favorably about the Drude model several times on PF. Nevertheless, I fear citing it because of some comments I've seen on PF that make Drude sound deprecated like relativistic mass.

The simple classical Drude model I described above is only a crude heuristic model!

In 1900, there was something called the Drude model, which attempted to do this. It got Ohm's Law as an output (sort of) and pretty much got everything else wrong.

 

[sophiecentaur]

Summary: Does Ohm's Law work for Light Bulbs? I did a simple experiment where it doesn't seem to.

this is the only explanation I can think of off the top of my head of why Ohm’s law does not work for a lightbulb.

Exactly. Ohm's law describes the behaviour of metals at constant temperature - same as Boyle's Law assumes constant temperature and Charles' Law assumes constant pressure.

I never understand why people refer to the definition of Resistance as Ohm's law. (Actually, I can understand why; it's because sloppiness propagates when it's convenient). Everywhere you look, they say things like "By Ohm's Law, R=V/I" which is nonsense, when you think about it. The ratio of V/I is defined as R to enable all those circuit calculations to work and any element that is actually conducting a current can be said to have a 'Resistance' for any particular V across it. That's basically an 'Effective Resistance' and can't be relied on from one moment to the next - except when someone has gone to the trouble of making a resistive component with a very low temperature coefficient of resistance. You could say that it does better than Ohm's Law because it stays at '220Ω' even when it gets (slightly) hot.

I can't change the usage and so PF will forever be getting questions about it and students will lose sleep.

 

[Albertgauss]

Hi all,

Some background:

I’m not intending to “disprove” Ohm’s Law. From the experience of this post that I didn’t know beforehand, I will think better to reword phrases like “Ohm’s Law doesn’t work for...”

The materials I use here are all standard, cheap, physics education stuff on the shelf of any storeroom for a classroom, which you all know from when you were students going through the physics introductory series in college. No, I am not claiming any new physics here.

I am doing something similar to drmalawi steps 1,2,3,4

Basically, I prepared some activities for students in a class with regular resistors and Ohm’s Law works great for them. Then, thinking that the demo light bulbs we have on the shelf wouldn’t be demo light bulbs unless they conformed to Ohm’s Law, I was quite surprised how much they did not adhere to Ohm’s Law as how the resistors did. I was going to use the light bulbs in an activity as “real-world” devices as examples of Ohm’s Law; but obviously I can’t do that because they behaved much differently than I expected. The point of this post was to see if I overlooked something major on Ohm’s Law since I had been so sure the light bulbs should have had an easy dependence on Ohm’s usual Law, V = IR. I realize now that Ohm’s Law applied to demo light bulbs is not straightforward.

I don’t want to get technical if Ohm’s Law is a “Law” or “Rule” or “theory”. I know it is used for at least demo resistors and that’s is really what I am using it for.

I am quite satisfied with simple answers such as: 1) Light bulbs are far from ideal resistors, 2) The light bulb is non-linear, 3) Light bulb resistance is a function of temperature (without the math), 4) Ohm's law describes the behaviour of metals at constant temperature. A consensus of these reasons by the group as reasons to explain my experiments is perfect enough for me to say the post is completely answered.

For this post, I am not concerned with AC anything, any kind of diodes, MOVs, gas discharge tubes, some polymers, no Maxwell differential calculus, I’m not doing a continental power grid either, no quantum, we won’t be doing Taylor series for this. Such points are surely correct and valid, but I’m not going to into these topics at this time Ohm’s Law.

I do actually appreciate everyone giving attention to this; I did learn a lot of useful things I did not know before.