Does the Circular Twin Paradox Challenge Our Understanding of Time Dilation?

[JVNY]

Here is a scenario in which two twins age at different rates even though both always have the same speed.Consider a train track that includes a circular segment with ground circumference minutely greater than 80. Two twins are on a train with synchronized watches (Frank at the front and Reba at the rear). The train has proper length 100 and velocity in the inertial ground frame of 0.6c. While traveling inertially (point 1 in the diagram below), in the ground frame the train’s length is 80 and Reba’s watch is ahead of Frank’s by the product of the train’s proper length and its speed, or 60. The tracks shunt the train into the circular segment as it passes. After completing the circuit around the circle, the front of the train exits just as the rear has entered, and Frank grazes Reba (point 2 in the diagram below). At this event, they compare watches. Each has traveled at the same speed the entire time (0.6c), and therefore Reba’s watch remains 60 ahead of Frank’s in the ground frame. Because they are both at the same event, Reba is 60 older than Frank. Frank has aged 60 less than Reba during his circuit.

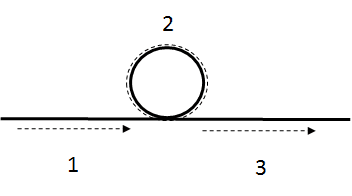
Thereafter Frank and the front of the train travel inertially to the right; Reba and the rear of the train complete the circuit, exit the circle, and then continue inertially to the right (point 3 in the diagram). Each watch has continued to travel at the same speed; Reba’s watch continues to be 60 ahead of Frank’s in the ground frame; but their watches are now synchronized again in their inertial frame. Reba has aged 60 less than Frank during her circuit.In this scenario the twins age at different rates during their travels even though they always travel at the same speed. The change of direction acceleration within the circle causes the different aging. Speed has an impact, but only on the amount of differential aging during acceleration (the product of the train’s proper length and speed). The proper length has an important role also. If you double the proper length of the train and the ground circumference of the circle while maintaining the train’s speed at 0.6c, you double the time during which the train undergoes change of direction acceleration, and you double the amount of differential aging that occurs during the acceleration – even though the twins continue to travel at the same speed at all times, and it is the same speed (0.6c) as they traveled on the shorter circumference.I’d appreciate your general thoughts on the scenario and any specific views you can offer on which twin’s worldline is longer during the period between Frank entering the circle and his grazing Reba. Presumably his worldline is a helix and hers is a straight line; each travels the same distance in the ground frame over the same time in the ground frame; but I do not know how one measures each worldline to determine which is longer, and what the measure of each is.

Thanks.

 

[PeterDonis]

which twin’s worldline is longer during the period between Frank entering the circle and his grazing Reba.

The two worldlines are the same length, since both of them experience the same lapse of proper time (same speed in the ground frame, same distance covered in the ground frame), and proper time is the length of the worldline.

 

[pervect]

I'm a bit confused. If we consider a frame co-moving with the train - then the train's velocity isn't constant. The train's velocity in the lab frame is constant, but that's not the synchronization convention that observers on the train would use.

So if I understand the scenario properly, the times on the train clock are different, but it's due to the fact that the velocity in the train frame wasn't constant.

 

[A.T.]

Two twins are on a train with synchronized watches (Frank at the front and Reba at the rear).

Synchronized in which frame? Train or ground?

 

[Ibix]

Let the origin be Frank crossing the points for the first time. In the ground frame, then, his x and y coordinates in terms of t are:$$\begin{eqnarray*} x&=&R\sin(vt/R)\\ y&=&R-R\cos(vt/R) \end{eqnarray*}$$where R is the radius of the track and v is the speed of the train. Then you can write $$dx = \frac{\partial x}{\partial t}dt = v\cos(vt/R)dt$$and similarly $dy=v\sin(vt/R)dt$. That let's you write that $$d\tau^2 = dt^2-dx^2-dy^2 = (1-v^2)dt^2$$You can trivially integrate $d\tau$ over the period Frank is in the circle, or just note that Frank's proper time has the same ratio to t as Reba's does. Either gives you the result Peter stated in #2.

The reason that their clocks drift in and out of sync in the inertial frame of the straight bit of the train is that while they are going round the circle they are changing simultaneity conventions in a non-trivial way. I think this is related to what happens in Bell's paradox, where clocks at the nose and rear of a rocket initially synchronised in its rest frame are not synchronised after a period of acceleration.

 

[A.T.]

To me the issue is that they don't have two meetings, to compare proper time intervals between them locally.

But let's say there are two such loops along the track. If they keep the same speed between the two meetings, they will register the same proper time interval between them.

 

[JVNY]

Great comments, thanks. I will go over them separately. The main issue to keep in mind is whether the scenario shows that acceleration rather than speed causes the differential aging. The standard view is that speed, not acceleration, causes differential aging.

Synchronized in which frame? Train or ground?

Initially synchronized in the train frame.

To me the issue is that they don't have two meetings, to compare proper time intervals between them locally.

However, they both start in the same inertial train frame with synchronized watches, so we know how their proper times begin. They can also send signals to each other to Einstein synchronize their watches while they are inertial. Then they meet when Frank grazes Reba, and they can compare their proper (wristwatch) times then to determine the lapse of each's. You can even assume that they were born at the center of an always-inertial train, then were carried at the same time at the same speed measured in the train frame to the opposite ends of the train, so that at all times their bodies aged at the same rate before Frank entered the circle.

The two worldlines are the same length, since both of them experience the same lapse of proper time (same speed in the ground frame, same distance covered in the ground frame), and proper time is the length of the worldline.

But in fact they experience a different lapse of proper time in this specific period. Frank's proper time lapses 60 less than Reba's between the point at which Frank enters the circle (watches are synchronized in a shared inertial frame) and the point at which he grazes Reba (both observers present at the same event, and her wristwatch ahead of his by 60).

How does one measure the worldlines? Using a Minkowski diagram based on the ground frame? Then in that case do you measure the length of each's worldline in the three spacetime dimension diagram (x and y for space, ct for time)? Reba's worldline starts out to the left of Frank's and ends up grazing his but is always straight. His curves.

But is it even correct to use the inertial ground frame as the base for the diagram? As discussed more below, there are issues with simultaneity and simultaneity conventions for Frank and Reba, so is it correct to measure their worldlines in a frame that always has a single simultaneity surface?

I think this is related to what happens in Bell's paradox, where clocks at the nose and rear of a rocket initially synchronised in its rest frame are not synchronised after a period of acceleration.

I agree. Or, perhaps it is like what happens in Born rigid acceleration, where clocks initially synchronized in their rest frame also desynchronize (although rearward clocks fall behind in these cases, but the front clock falls behind in this scenario -- perhaps this scenario is more like a negative acceleration version of Bell's paradox or Born rigid acceleration). In Bell's case the front and rear move apart (any physical object connecting them like a thread is pulled apart), whereas in Born rigid acceleration they maintain their same distance in their own frame (any physical object connecting them remains undeformed).

So if I understand the scenario properly, the times on the train clock are different, but it's due to the fact that the velocity in the train frame wasn't constant.

Do you mean magnitude or direction of velocity? I believe that both Frank and Reba measure their magnitude of velocity relative to the track as 0.6c. I suspect that they do agree that they do not have the same direction of velocity during this restricted period. This gets to the central point here. Does the twin paradox depend on speed (magnitude of velocity) or acceleration (in this case, change of direction acceleration)? It seems that whether a ground observer or a train observer measures speed, the relative speed of a train observer to the ground and a ground observer to the train is always 0.6c. Yet in the specified period one twin accelerates (Frank -- he changes direction), and the other does not (Reba -- she continues to travel inertially to the right). And the twin who accelerates ages less.

If we consider a frame co-moving with the train - then the train's velocity isn't constant. The train's velocity in the lab frame is constant, but that's not the synchronization convention that observers on the train would use.

I know from prior posts that there is a whole can of worms involved in defining the train's frame when it moves in a circle. I assume that it is even messier when part of the train is moving in a circular way (the front after Frank has entered the circle) and part is still moving in a straight line (before Reba enters the circle). Also, it follows from other threads that there is no shared simultaneity surface on the train once the front starts to move in a circle, and train observers cannot Einstein synchronize their clocks in the circle. So would any synchronization convention that Frank and Reba agree upon matter?

The reason that their clocks drift in and out of sync in the inertial frame of the straight bit of the train is that while they are going round the circle they are changing simultaneity conventions in a non-trivial way.

Agreed, and repeating a line from just above, Frank and Reba do not share a simultaneity surface in this restricted period, so any convention that they use might have limited value.

It seems that Frank's circular motion allows the twins to go from a shared simultaneity surface that differs from that of the ground frame to a simultaneity point that is the same for them and the ground frame. And during the change of direction acceleration Frank ages less, even though both twins always have the same speed.

 

[A.T.]

Initially synchronized in the train frame.

If the clocks initially show the same time in the train frame, then they have an offset in the ground frame. That is also the offset they will see at their meeting, because the ground frame always sees them at the same speed and thus same tick rate.

 

[PeroK]

Here is a scenario in which two twins age at different rates even though both always have the same speed.

The first thing I didn't understand is why they had to be twins. If they are travelling, some distance apart, relative to an observer, then to that observer they are not twins.

The whole twins thing is a red herring. Concentrate on the watches instead.

First, look at the motion from Reba's frame. The track comes along, picks up Frank, circles him round and drops him at her feet! Originally their watches were synchronised in their frame, but now his watch is behind in their frame.

From the ground frame: initially Frank's watch was behind. Both watches progressed at the same rate while Frank did his loop-the-loop, so Frank's watch was still behind by the same amount when he landed at Reba's feet.

 

[PeterDonis]

The standard view is that speed, not acceleration, causes differential aging.

No, the standard view is that a difference in the length of worldlines causes differential aging. But what you are observing here is not differential aging; it is simply the fact that the two clocks are not synchronized in the ground frame--Reba's clock is set ahead of Frank's clock. Both clocks tick at the same rate in the ground frame, so both Reba and Frank age at the same rate. It just so happens that their worldlines cross at one event because of the non-inertial segment in each of them, so the fact that Reba's clock is set ahead of Frank's becomes locally observable.

 

[pervect]

But is it even correct to use the inertial ground frame as the base for the diagram? As discussed more below, there are issues with simultaneity and simultaneity conventions for Frank and Reba, so is it correct to measure their worldlines in a frame that always has a single simultaneity surface?

You can perform a correct analysis in any frame you choose, but you have to pick one particular frame and stick with it. It's easiest to use an inertial frame, more generally you can pick any coordinate system you choose and use the techniques of General Relativity with an appropriate metric. But let's stick with inertial frames as that's the easiest approach.

If you perform the analysis in the inertial ground frame, the problem is perhaps easiest to solve. In that frame, which I will call the lab frame, Frank and Reba's clocks were never synchronized. Their synchronization state remain unchanged, as they traverse the loop. They start out unsyncronized, remain unsyncronized by the same amount throghout their travels. So there will be a constant time difference (in that frame), it will be the same before frank enters the loop, when frank meets reba, and when reba has also gone through the loop. Of course, Frank and Reba are at the same point in space only at one point, the point where they meet, otherwise they are never both in the same spot at the same time.

If you perform an analysis in the frames that are represented by 1 and 3 in your diagram, an inertial frame co-moving with the train (i.e moving to the right on the diagram), you get the same answer to physical prediction of what happoens when they meet up, but the explanation is different. In that frame, then the clocks start out synchronized. However, the train's velocity in that frame is NOT constant as it traverses the loop (it starts out as zero at the bottom of the loop, and becomes negative at the top of the loop, returning to zero again when the train reaches the bottom again). So in that frame the clocks start out synchronized, become unsyncronized when Frank goes through the loop due to Frank's non-constant velocity profile. The clocks then become re-synchronized when both Frank and Reba have gone through the loop.

No matter which approach you take, you get the same prediction, that Frank and Reba's clock do not read the same when they meet.

 

[JVNY]

But what you are observing here is not differential aging; it is simply the fact that the two clocks are not synchronized in the ground frame

Actually I am describing differential aging. Frank and Reba are twins and have the same age at the outset in their shared inertial train frame. After Frank completes the circuit and grazes Reba, he is younger than she is by 60. He has undergone time dilation; his watch and his body clock have ticked more slowly than hers. As PeroK and pervect note:

Originally their watches were synchronised in their frame, but now his watch is behind in their frame.

So in that frame the clocks start out synchronized, become unsyncronized when Frank goes through the loop due to Frank's non-constant velocity profile.

And time dilation is generally explained by speed. Per the Physics FAQs site,

a "clock will count out its time in such a way that at anyone moment, its timing has slowed by a factor (γ) that depends only on its current speed" see http://math.ucr.edu/home/baez/physics/Relativity/SR/clock.html​

No, the standard view is that a difference in the length of worldlines causes differential aging.

This is another way of describing it, true. And some people describe both ways, like DaleSpam in post number 10 here:

"You can either say that velocity causes time dilation or that time dilation is just what happens when a clock takes a shorter path through spacetime. I prefer the second approach, which is the spacetime geometric explanation."

Does acceleration cause time dilation?​

So let's go with the worldline approach. How long is the worldline of each starting at the point at which Frank enters the circle through the point at which he exits the circle and grazes Reba as she has entered the circle? Can anyone calculate the actual length of each worldline? That would really help.

 

[PeterDonis]

Frank and Reba are twins and have the same age at the outset in their shared inertial train frame.

But they aren't spatially co-located in that frame, so there is no absolute sense in which they "have the same age"; their "age" as you are using the term is frame-dependent. Differential aging is an absolute--you have two twins who start out spatially co-located, so their relative age at that point is an absolute, invariant fact; then they separate, then they come back together, so they are spatially co-located again, and their relative age has changed, again as an absolute, invariant fact. This never happens in your scenario; Frank and Reba are only spatially co-located once, when Frank is exiting the circular shunt and Reba is entering it.

You could modify your scenario to add a second event at which they are spatially co-located: just add a second circular shunt. The simplest way is to put it a distance of 80 down the track from the first shunt, so Frank enters the second shunt, in the ground frame, at the instant Reba is exiting the first shunt. Then Frank and Reba will be spatially co-located again when Frank exits the second shunt and Reba enters it: and, what's more, they will see that they have both aged by the same amount between their two meetings. So once we add a second meeting to your scenario to evaluate differential aging, we see that there isn't any.

 

[Dale]

Actually I am describing differential aging.

I agree with Peter Donis here. What you are describing is not what is usually meant by differential aging. Differential aging is invariant and requires the two clocks to be colocated at the beginning and at the end of the measurement.

Your scenario is completely valid, but it is not differential aging.

 

[PeterDonis]

How long is the worldline of each starting at the point at which Frank enters the circle through the point at which he exits the circle and grazes Reba as she has entered the circle? Can anyone calculate the actual length of each worldline?

The length of the worldline is just the proper time elapsed for the observer following the worldline. So since each person has elapsed time of 60 between the points you mention, the length of each worldline between the given points is 60. So they're the same.

 

[pervect]

And time dilation is generally explained by speed. Per the Physics FAQs site,

a "clock will count out its time in such a way that at anyone moment, its timing has slowed by a factor (γ) that depends only on its current speed" see http://math.ucr.edu/home/baez/physics/Relativity/SR/clock.html​

I'm not sure what your point is. I already pointed out that in the frame where the speed is constant, which I call the lab frame, the time dilation is constant. And that in the frame that I call the train frame, the speed isn't constant and the time dilation isn't constant either. This is total consistent with the FAQ entry you quote, and your remarks. So I'm at a bit of a loss to be sure of what you think we disagree about, if anything. If I take your remarks at face value we are agreeing, but the context leads me to believe otherwise.

Do you agree that your scenario is consistent with "time dilation being due to speed"? If you do agree, then I don't see whatstill nee ds to be discussed. If you don't agree, you might want to re-think why, and explain in a post.

So let's go with the worldline approach. How long is the worldline of each starting at the point at which Frank enters the circle through the point at which he exits the circle and grazes Reba as she has entered the circle? Can anyone calculate the actual length of each worldline? That would really help.

The length of a timelike worldline is just a proper time interval, symbolized by $\tau$. If we are doing special relativity in Minkowskii coordinates (t,x,y,z), the formula for the length of a timelike worldline is $\int d\tau$ where $d\tau =\sqrt{dt^2 - dx^2 - dy^2 - dz^2}$. Dividing both sides by dt, we come up the relation that

$$\Gamma = \frac{d\tau}{dt} = \sqrt{ 1 - (\frac{dx}{dt})^2 - (\frac{dy}{dt})^2 - (\frac{dz}{dt})^2}$$

[add] I need to note that I assumed that c=1, i.e. this is all in geometric units.

So $d\tau$ is an infinitesimal length, the length of a finte cure is $\int d\tau = \int \Gamma dt$

Any observer computes the same value for $d\tau$, regardless of their frame of reference. DIfferent observers do not necessarily agree on the value of $\gamma$ though, $\gamma$ depends on the choice of frame of reference.

I am concerned that we both understand what the variables $t,x,y,z$ and $\tau$ represent, why $d\tau$ is "the length of an infinitesimal part of a curve", and why $dt / d\tau$ is "time dilation". If there's something unclear about all this, please try and mention it.

Additionally, it might also be useful to note that the formula explicitly state that "time dilation" i.e. $\Gamma$ is a function of velocity $dx/dt$, $dy/dt$, $dz/dt$ and not acceleration (i.e. $d^2 x / dt^2$, etc.).

 

[PeroK]

I agree with Peter Donis here. What you are describing is not what is usually meant by differential aging. Differential aging is invariant and requires the two clocks to be colocated at the beginning and at the end of the measurement.

Your scenario is completely valid, but it is not differential aging.

I don't think the scenario is valid at all. The opening gambit was:

Here is a scenario in which two twins age at different rates even though both always have the same speed.

(Presumably we are talking about the ground frame here.)

The OP believes that they age differently in the ground frame, even though they travel at the same speed in the ground frame and therefore there is time dilation due to acceleration, not speed.

But, as has been pointed out in several posts now, the flaw is that they do not start out the same age in the ground frame. The whole scenario is based on the elementary falacy that the "twins" are the same age in both frames at the outset.

 

[Dale]

But, as has been pointed out in several posts now, the flaw is that they do not start out the same age in the ground frame. The whole scenario is based on the elementary falacy that the "twins" are the same age in both frames at the outset

Yes I do agree with that. I was not saying that his analysis of the scenario was right, just that the scenario was one that was possible to analyze. I.E. it didn't involve anything non-physical such as FTL or perfect rigidity.

 

[JVNY]

Thanks all. I think that the main disagreement is that I consider the twins to have the same age in the beginning inertial stage because they share the same simultaneity surface, so when they meet at the same point you can directly compare their ages then with their ages on the original simultaneity surface. But this appears to be incorrect.

But they aren't spatially co-located in that frame, so there is no absolute sense in which they "have the same age"; their "age" as you are using the term is frame-dependent.

I thought that when two observers are in the same inertial frame then there is an absolute sense as between them in which they have the same age.

The OP believes that they age differently in the ground frame

No, I believe that they age differently relative to each other as twins, not that they age differently in the ground frame. They clearly age the same in the ground frame.

Say they are two artificial people born at the same train frame time on opposite ends of the train and they have the same pre-determined lifetime measured by an ideal built in body clock (say 160). Then they can communicate with each other throughout their lives and will die at the same time on the train. Neither can possibly see the other die as long as they both remain inertial. But in the scenario I described, Frank would live 60 longer than Reba, so if they meet when her body clock reads 160 then his reads 100, and he will see her die. This is the absolute sense of aging as between the two of them that I am referring to. I do not understand why Frank's longer life is any less absolute as between the two of them than if they had begun together at a single point.

I already pointed out that in the frame where the speed is constant, which I call the lab frame, the time dilation is constant. And that in the frame that I call the train frame, the speed isn't constant and the time dilation isn't constant either.

But what about Frank and Reba's speeds? Is it not the case that Frank and Reba will each always measure his/her speed to be 0.6c relative to the lab frame? Frank undergoes change of direction acceleration, but he does not undergo change of speed acceleration. If a lab observer always measures his speed relative to the lab as 0.6c, then he must also measure his speed relative to the lab as 0.6c. This is what I mean by them always having the same speed, thus the fact that Reba dies before Frank is caused by acceleration, not speed. Is there some other measure of speed, such as a speed that Frank and Reba measure as between themselves, in which they have different speeds? I am not sure why I don't understand this the same way that all of you do, but I suspect that it involves what pervect is saying about the speed in the train frame.

However, the train's velocity in that frame is NOT constant as it traverses the loop (it starts out as zero at the bottom of the loop, and becomes negative at the top of the loop, returning to zero again when the train reaches the bottom again).

I am still trying to understand this. Are you referring to magnitude or direction of velocity? If we consider Frank, it seems that he has always a constant magnitude of velocity (0.6c); it is just his direction of velocity that changes while he is in the loop. And Reba is always inertial with magnitude of velocity 0.6c before the two meet.

So since each person has elapsed time of 60 between the points you mention, the length of each worldline between the given points is 60.

I agree as to the ground frame. But I am trying to consider as between Frank and Reba. Perhaps this is just not possible to do unless they begin co-located.

You can perform a correct analysis in any frame you choose, but you have to pick one particular frame and stick with it.

I understand how to do it in the inertial lab frame, and I see that their clocks tick at the same rate. They do not start co-located, but it seems theoretically possible to determine their worldlines in that frame. I think that everyone is suggesting that their worldlines in that frame are the same length (because both of their clocks tick the same amount in that frame).

Does that mean that they have the same length worldlines in all frames? I thought that that was the case. I can see where their worldlines end in all frames (when they meet); I am now confused on where their worldlines begin in any frame other than the lab frame (where they begin 80 apart in space), because it seems that I cannot compare their ages at the start of the scenario. I could start them at 100 apart in space and 0 apart in time in the train frame each with the same body clock time, but I fear that that looks as if I think that they have the same absolute age at the start, which seems not to be the case.

 

[PeroK]

Thanks all. I think that the main disagreement is that I consider the twins to have the same age in the beginning inertial stage because they share the same simultaneity surface, so when they meet at the same point you can directly compare their ages then with their ages on the original simultaneity surface. But this appears to be incorrect.

How is your scenario any different from one when one of the twins makes a high-speed journey to join the other? The twins thing is misleading, because if you're considering relativistic velocities, anything could have happened during their lifetimes to give them different ages, whether colocated or not.

Instead, simply consider their initially synchronised watches in their initial inertial reference frame, where they are relatively at rest. One of them makes a journey to the other and thereby experiences less proper time than the one who remains inertial.

 

[jbriggs444]

Thanks all. I think that the main disagreement is that I consider the twins to have the same age in the beginning inertial stage because they share the same simultaneity surface, so when they meet at the same point you can directly compare their ages then with their ages on the original simultaneity surface. But this appears to be incorrect.

The "simultaneity surface" is not a feature of the twins. It is a feature of a reference frame in which they happen to both be at rest.

I thought that when two observers are in the same inertial frame then there is an absolute sense as between them in which they have the same age.

It is still only a frame-dependent sense. The twins are also "in" the lab frame. What they are not is "at rest in" the lab frame.

No, I believe that they age differently relative to each other as twins, not that they age differently in the ground frame. They clearly age the same in the ground frame.

Neither twin is always at rest in any single inertial reference frame. For the accelerated portion of their journey they are momentarily at rest in a sequence of inertial frames each at a slightly different velocity relative to the one before. If a twin adopts a point of view that continuously jumps from one momentarily co-moving inertial frame to the next then the continuous shifting affects the chosen surface of simultaneity and, consequently, affects the rate of time passage that is computed for the peer twin.

It is not that the acceleration affects the local twin's clock. Experiment shows that proper acceleration does not affect clocks. It is not that the local twin's acceleration affects the remote twin's clock. How could it?. It is that acceleration affects the notion of simultaneity. Some notion of simultaneity is necessary in order to compare the tick rate of a clock over here with the tick rate of a clock over there. If you adopt a changing notion of simultaneity, strange things will seem to happen to clocks.

 

[PeterDonis]

I think that the main disagreement is that I consider the twins to have the same age in the beginning inertial stage because they share the same simultaneity surface

As others have pointed out, that is not an absolute meaning of "the same age"; it's frame dependent, and any age relationship determined by this criterion will change if either twin moves non-inertially. If you really want to think of "age" as an absolute, you have to think of it as belonging to a specific observer at a specific event on their worldline, and that's it. That is: Reba and Frank each have a clock that shows a certain reading at each event on their worldlines; the difference between the readings of that clock between two events on their worldlines tells you how much they aged. So, for example, if Reba's clock reads zero at the event where her end of the train (the rear end) is a distance 80 from the shunt, in the ground frame, and her clock reads 60 at the event where her end of the train is just entering the shunt (this is the event where she is co-located with Frank), then she has aged by 60 between those two events.

If you want to compare Reba's and Frank's "ages", however, you have to know at which event on Frank's worldline Frank's clock reads zero. As you specified the problem, that event is the event where Frank's end of the train is just exiting the shunt--i.e., the event where Frank is co-located with Reba. That is because you specified that Frank's clock runs 60 behind Reba's as seen from the ground frame, so at the event where Frank's end of the train is just entering the shunt, Frank's clock must read minus 60, since that event, in the ground frame, is simultaneous with the event, given above, at which Reba's clock reads zero. And Frank's clock advances by 60 while he is in the shunt, so when he exits the shunt, his clock must read zero--60 behind Reba's clock. So Frank is 60 "younger" than Reba by this criterion. But that depends on specifying a particular event on Frank's worldline as being the one at which his clock reads zero; a different specification of that would lead to different relative "ages" for Frank and Reba when they meet. And since they only meet once, there is no absolute way to specify their relative ages.

In my alternate scenario, however, where Frank and Reba meet twice, it is possible to give an absolute meaning to their relative ages, because we can assess the change in both of their clocks between the two meetings, which is an absolute. And we find, as I showed, that both of their clocks change by the same amount between the two meetings. So in this absolute sense, Frank and Reba age at the same rate.

I thought that when two observers are in the same inertial frame then there is an absolute sense as between them in which they have the same age.

Nope. See above.

Say they are two artificial people born at the same train frame time on opposite ends of the train and they have the same pre-determined lifetime measured by an ideal built in body clock (say 160). Then they can communicate with each other throughout their lives and will die at the same time on the train. Neither can possibly see the other die as long as they both remain inertial. But in the scenario I described, Frank would live 60 longer than Reba.

No, he wouldn't. They would both live for 160 units of time. What you mean is, Frank would see Reba die. But that is because of the way you specified when each of their clocks started--at which event they were born--and how they moved. Suppose, for example, that Frank is born just as his end of the train enters the shunt. As you have specified the relationship between the births, that means Reba would be age 60 when her end of the train is a distance 80 from the shunt, in the ground frame (the event at which, in my discussion above, I had her clock reading zero--but now we're talking about a different specification for the zero points of the clocks). So Reba would be age 120 when she meets Frank, as she is entering the shunt and he is exiting it, and Frank would be age 60 at that event. So obviously he is going to see her die, because she was born earlier--at least, "earlier" in the only possible absolute sense at this point, since they only meet at this one event (Reba will reach age 160 and die before she even exits the shunt).

Also, as should be evident, Reba and Frank will not die "at the same time" in the original train frame either, because both of them will have moved non-inertially, and for different amounts of time by their clocks, by the time they die, so their death events will no longer be simultaneous in the original train frame, even though their birth events were. You can use an inertial frame to describe non-inertial motion, but you can't just assume that all of the same simultaneity properties will hold.

Is it not the case that Frank and Reba will each always measure his/her speed to be 0.6c relative to the lab frame?

Yes, it is.

the fact that Reba dies before Frank is caused by acceleration, not speed

No, it's caused by the frame-dependent definition of "before" that you used. Since Reba and Frank only meet once, the only possible absolute sense you can give to their relative ages is their relative ages when they meet; and by that criterion, as above, Reba dies before Frank because she was born before Frank. Since both their birth and death events are spacelike separated, there is no absolute way to determine which happened first.

I agree as to the ground frame.

Lengths of worldlines between two given events are invariants; they are the same in all frames.

 

[pervect]

Thanks all. I think that the main disagreement is that I consider the twins to have the same age in the beginning inertial stage because they share the same simultaneity surface, so when they meet at the same point you can directly compare their ages then with their ages on the original simultaneity surface. But this appears to be incorrect.

...

I thought that when two observers are in the same inertial frame then there is an absolute sense as between them in which they have the same age.

If two observers are in the same inertial frame, it is natural to use that frame to define simultaneity and hence their age using that frame. While it is a "natural" choice, it's not "absolute". Just because it's "natural" to use that frame doesn't mean that it's required, or an absolute. There may be occasions when it is convenient to carry out the analysis in another frame besides the one that the two observers share. In the example we have been discussing, for instance, you seem to want to carry out the analysis in the lab frame because the speed of the observers is constant in that frame. That's fine, but the lab frame has a different notion of simultaneity and hence "age" than the shared frame. Simultaneity is never absolute, each different inertial frame has its own notion of simultaneity. You might find it helpful to review Einstein's original train paradox on this point.

But what about Frank and Reba's speeds? Is it not the case that Frank and Reba will each always measure his/her speed to be 0.6c relative to the lab frame?

Yes.

Frank undergoes change of direction acceleration, but he does not undergo change of speed acceleration. If a lab observer always measures his speed relative to the lab as 0.6c, then he must also measure his speed relative to the lab as 0.6c. This is what I mean by them always having the same speed, thus the fact that Reba dies before Frank is caused by acceleration, not speed. Is there some other measure of speed, such as a speed that Frank and Reba measure as between themselves, in which they have different speeds? I am not sure why I don't understand this the same way that all of you do, but I suspect that it involves what pervect is saying about the speed in the train frame.

See my previous remarks. The speed in the lab frame is indeed constant. Because the speed is constant in that frame, easier to carry out the analysis in that frame than in the moving inertial frame that Frank and Reba share. But in order to carry out the analysis in that frame, you need to understand that it has a different notion of simultaneity than the frame Frank and Reba share, because the notion of simultaneity itself depends on the frame you choose.

The other approach, which I've also mentioned, is to do the extra work and carry out the analysis in the shared frame. Note that the speed of the train is not constant in the shared frame, as I've also mentioned a few times before. It's more work, but if you need to see the analysis in the shared frame, it's perfectly do-able. It's often helpful to work a problem out several different ways to be sure you get the same answer, as well.

It appears to me that you are having some difficulty realizing that simultaneity depends on the frame, and this is where you're going wrong. It might be helpful to review Einstein's original train experiment with the straight track before trying to understand how it works with the curved track.

See for instance http://www.bartleby.com/173/9.html

Another paper that attempts to deal with the issue I believe you're struggling with is: Scherr's paper "The challenge of changing deeply-held student beliefs about the relativity of simultaneity". http://arxiv.org/abs/physics/0207081

If you do read Scherr's paper, I'd be interested in whether it helps you or not. So far I don't have any confirmed cases of people actually reading the paper, much less reading it and having it help them. But it seems to me to be a good paper and one that addresses the issues you're trying to come to terms with. And Scherr has reported reasonably good success rates using the techniques in his paper in teaching his students. Anyway, good luck.

 

[PeterDonis]

the moving inertial frame that Frank and Reba share

There is no such frame for the entire scenario, because Frank and Reba both move non-inertially for a portion of the scenario. I know you know this, but I'm not sure the OP understands the implications.

carry out the analysis in the shared frame. Note that the speed of the train is not constant in the shared frame

Now I'm confused; what "shared frame" are you talking about? There is no frame, not even a non-inertial one, in which Frank and Reba are both at rest all the time; that's impossible since they are spatially co-located at one event but not anywhere else.

In general, I don't think the notion of "frames" is a good one to focus on here; I think the invariant lengths of worldlines is better. But that's a matter of pedagogy, and pedagogy has to depend on the person who is trying to learn.

 

[DrGreg]

Now I'm confused; what "shared frame" are you talking about? There is no frame, not even a non-inertial one, in which Frank and Reba are both at rest all the time; that's impossible since they are spatially co-located at one event but not anywhere else.

I'm sure pervect must mean the inertial frame in which both Frank and Reba are both initially at rest and also both finally at rest. There are periods in between when either Frank or Reba (but never both) are not at rest in this inertial frame.

 

[PeterDonis]

I'm sure pervect must mean the inertial frame in which both Frank and Reba are both initially at rest and also both finally at rest.

Even here there are complications, because the relationship of both Frank's and Reba's clocks to the clocks in this inertial frame changes during their periods of non-inertial motion. So even though they start and end at rest in this frame, their clocks do not remain synchronized with a clock that is always at rest in this frame.

 

[JVNY]

Ok, I think that I am beginning to understand.

You can perform a correct analysis in any frame you choose, but you have to pick one particular frame and stick with it.

This means that if I refer to the speed of Frank and Reba in the inertial lab frame, I must stick with the lab frame for all observations. Since they have 0.6c speed everywhere in the lab frame, I must draw their worldlines in that frame. In that frame their worldlines have the same length because each ages the same amount in that frame. Reba's is a straight line (sloped to the right for the 0.6c rightward velocity); Frank's is a helix; but the lengths are the same.

If I refer to the train frame then . . .

It's easiest to use an inertial frame, more generally you can pick any coordinate system you choose and use the techniques of General Relativity with an appropriate metric. But let's stick with inertial frames as that's the easiest approach.

Well, better not to use the train frame, because different parts of the train are going around the loop at different times, so that is likely to be a very difficult frame.

So I will use an inertial frame co-moving with Reba to the right.

Instead, simply consider their initially synchronised watches in their initial inertial reference frame, where they are relatively at rest. One of them makes a journey to the other and thereby experiences less proper time than the one who remains inertial.

So, Frank starts out in that co-moving inertial frame, but then he leaves it when he goes in the circle and journeys to meet Reba. I simply ignore the ground frame entirely and just consider the inertial frame co-moving with Reba. In that frame, she is always at rest; Frank undergoes change of speed and change of direction:

First, look at the motion from Reba's frame. The track comes along, picks up Frank, circles him round and drops him at her feet!

In this frame, his clock runs slower than hers. His worldline is longer than hers.

How is your scenario any different from one when one of the twins makes a high-speed journey to join the other?

I will try to answer this based on the explanations by the various posters.

In the original twin paradox the two twins start co-located. One makes a high-speed journey out and back (or around and back), then returns to co-locate with the other. My scenario is different in that the two start out not co-located.

When I draw the worldlines of the two in the lab frame, I have to have a starting event for each worldline. Say I start with Reba 80 away from the shunt and Frank, with her clock ahead of his by 60. She starts at a different event from him (separated as just described). They end at the same event (the two grazing). Their worldlines have the same length.

When I draw the worldlines in the inertial frame co-moving with Reba, the lines end at the same event as the ones drawn in the lab frame (the grazing). However, they start at different events: Reba at a place farther away from the shunt and Frank, and their clocks both reading the same. In this frame, Frank has a longer worldline; his clock runs slower. This is because of the different starting events (it cannot be because of the ending event, because each has the same ending event).

So the basic mistake that I made was thinking that being on the same simultaneity surface can be the starting point for their worldlines in all cases. I think that I confused being on the same simultaneity surface with being at the same event. I don't know whether this is a deep rooted inability to accept the relativity of simultaneity, or just inattentiveness to the definition of an event. I will read the Scherr paper and see.

In order to have an absolute, frame-independent comparison of the two worldlines, the lines must start and end at the same events -- which means that Frank and Reba must be co-located at the same event the beginning and the same event at the end of the lines. So the difference between my scenario and the original twin paradox turns out to be very significant.

 

[PeterDonis]

In that frame their worldlines have the same length

Their worldlines between two given events have the same length in every frame. Worldline length between a given pair of events is an invariant. What changes when you change frames is which events you evaluate the length between. See further comments below.

In this frame, his clock runs slower than hers. His worldline is longer than hers.

More precisely: if we consider events which are simultaneous in this frame (which are not the same as pairs of events that are simultaneous in the ground frame), we find that Frank ages less between two corresponding pairs of events. These events are:

(1) The event at which Frank enters the shunt. Frank's clock reads zero at this event. The corresponding event on Reba's worldline is the event at which her clock reads zero; at this event, she is not a distance 80 from the shunt in the ground frame, but further away, and the ground frame assigns a negative time coordinate to this event (see below for numbers).

(2) The event at which Frank exits the shunt. Reba's worldline also passes through this event, so it is the "corresponding" event for her as well, and her clock shows a higher reading than Frank's at this event (again, see below for numbers). So in this frame, we are looking at the same segment of Frank's worldline compared to what we looked at above in the ground frame (the helical segment that goes around the shunt), but a different segment of Reba's worldline compared to what we looked at above in the ground frame--a straight line segment that is longer than the ground frame one we picked.

Regarding numbers: it turns out that we have been making some erroneous assumptions about these, so I have given explicit calculations of the event coordinates in two frames: the ground frame, and the "initial" train frame, the one in which the train is at rest before anyone goes around any shunts. I have put the spacetime origin of both frames at the event where Frank enters the shunt.

The relative velocity of the two frames is $0.6$, so we have $\gamma = 1.25$ and $\gamma v = 0.75$. So the Lorentz transformation equations are (the ground frame is unprimed and the initial train frame is primed):

$$
x' = 1.25 x - 0.75 t
$$
$$
t' = - 0.75 x + 1.25 t
$$

The inverse transformations are:

$$
x = 1.25 x' + 0.75 t'
$$
$$
t = 0.75 x' + 1.25 t'
$$

The events are:

Event F0: The event where Frank enters the shunt; his clock reads zero at this event. This event has coordinates $(0, 0)$ in both frames.

Event R0: The event where Reba's clock reads zero. This event, by hypothesis, has coordinates $(-100, 0)$ in the primed frame, since the train's proper length is 100, so Reba is a distance 100 behind Frank at this event in the primed frame. The unprimed coordinates of this event are therefore $(-125, -75)$.

Event R1: The event where Reba is a distance 80, in the ground frame, from the shunt. This event has coordinates $(-80, 0)$ in the unprimed frame. It therefore has coordinates $(-100, 60)$ in the primed frame.

We can already see that something is wrong with the assumptions we have been making, by comparing the coordinates of events R0 and R1. Between these events, in the primed frame, Reba's clock advances by 60; but in the unprimed frame, there is only a distance 45 between these events (-125 to -80). We have been assuming, all through this thread, that Reba's clock would advance by 60 in the time it took her to cover a distance 80 in the unprimed frame; but now we can see that must be wrong--in fact, her clock advances by 60 in the time it takes her to cover a distance of only 45 in the unprimed frame. (Note that it takes her a time 45/.06 = 75 in the unprimed frame to cover this distance, and 75 divided by the time dilation factor of 1.25 is 60, so this works out.) We'll see further corrections when we look at the next event below.

Event F1: The event where Frank exits the shunt. Reba is just entering the shunt at this event. The question is, what are its coordinates? It seems like, in the primed frame, they should be $(-100, 120)$, because Reba is at $x' = -100$ and we assumed that her clock reads 60 elapsed time between event R1 and this one. But what does this transform to in the unprimed frame? It transforms to $(-35, 75)$. That can't be right, because this event should be at $x = 0$ in the unprimed frame, since the shunt entry and exit are at the same point in space in this frame, which is the spatial origin.

So we have to take a step back and re-evaluate, once again, how much time elapses on Reba's clock while she covers a distance 80 in the ground frame. The train is moving at $v = 0.6$, so it takes a time $80 / .06 = 133.33$ in the ground frame to cover that distance. So the coordinates of event F1 in the unprimed frame must be $(0, 133.33)$. In the primed frame, this transforms to $(-100, 166.67)$. So between event R1 and this event, Reba's clock advances by 106.67; and that is the unprimed time of 133.33 divided by the time dilation factor of 1.25, so once again it works out.

In other words, when Reba and Frank meet, Reba's clock does not read 120, as we have been (incorrectly) assuming all through this thread; it reads 166.67. We can see this another way: in the initial train frame, when Reba's clock reads zero, the shunt is a distance 100 away from her. But the shunt is moving at $v = 0.6$ in this frame, so it will take a time $100 / 0.6 = 166.67$ in this frame to reach Reba.

This also means that, when Reba and Frank meet, Frank's clock does not read 60, as we have been (incorrectly) assuming all along; it reads 106.67. We can see this from the above--it's the time in the unprimed frame that it takes to cover a distance 80 in that frame, divided by the time dilation factor of 1.25--but we also expect it because we know Frank's clock is 60 behind Reba's with respect to the ground frame.

So to sum up: in the ground frame, we are comparing the segment of Frank's worldline between events F0 and F1, with the segment of Reba's worldline between events R1 and F1. These segments both have length 106.67. But in the initial train frame, we are comparing the same segment of Frank's worldline (F0 to F1) with the segment of Reba's worldline between events R0 and F1, which has length 166.67.

This analysis appears to be basically the same as the rest of your post, just with the numbers made explicit (and the erroneous assumptions we were making about the specific numbers corrected).

 

[DrGreg]

So, Frank starts out in that co-moving inertial frame, but then he leaves it when he goes in the circle and journeys to meet Reba.

A small point about terminology. Rather than talking of being "in" a frame and then later "leaving" the frame, it's better to say that relative to the frame Frank is initially at rest and later moving. As a frame is just a coordinate system (at least in the sense we are using it here), everything is "in" every frame.

 

[JVNY]

Excellent, thanks to all.