Does this triangle have to be flipped when finding the magnitudes and angles?

[Raerin]

In those kind of relative velocity questions in calculus & vectors class, does the direction of the plane need to be flipped when drawing the triangle to find the magnitudes and angles?

Example of a question:
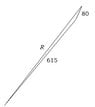
An airline pilot has her controls set to fly at an air speed of 615 km/h at an azimuth bearing of 40 degrees. A wind is blowing from an azimuth bearing of 205 degrees at 80 km/h. Determine the velocity of the plane relative to the ground.

For this question, I also have troubles finding the angles between vectors when I draw the triangle. A link to an illustration on Paint or some other drawing program would be really helpful!

Thanks :)

 

[MarkFL]

Here are two ways to work the problem:

a) Law of Cosines:

Consider the following diagram:

View attachment 1546

The angle between the plane's velocity vector and that of the wind is:

$$\theta=\left(180-((90-(205-180))-(90-40)) \right)^{\circ}=165^{\circ}$$

Hence:

$$R=\sqrt{615^2+80^2-2\cdot615\cdot80\cos\left(165^{\circ} \right)}\approx692.583642102$$

b) Vector addition:

$$\vec{R}=\left\langle 615\cos\left(50^{\circ} \right)+80\cos\left(65^{\circ} \right),\sin\left(50^{\circ} \right)+80\sin\left(65^{\circ} \right) \right\rangle$$

$$R=\left|\vec{R} \right|=\sqrt{\left(615\cos\left(50^{\circ} \right)+80\cos\left(65^{\circ} \right) \right)^2+\left(\sin\left(50^{\circ} \right)+80\sin\left(65^{\circ} \right) \right)^2}\approx692.583642102$$