- #1
randomgamernerd
- 139
- 4
Homework Statement
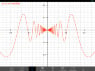
:[/B]limx->0xsin(1/x)
Homework Equations
: [/B]-The Attempt at a Solution
:[/B]I feel the limit does not exist. Because sin(1/x) is largely changing value as x approaches 0,(since it is an oscillating function), and in limit, we check what happens in neighborhood of the point in concern. Now for x= say 10-999 we might have y>0. But since sin(1/x) is rapidly changing values, so it might happen at x=10-999 +0.000001, y<0. so i guess the function is rapidly changing altitude. So i guess limit does not exist. But I notice in the graph that the amplitude of the function is tending towards zero, and at x=0 it is exactly equal to zero. But I still disagree on the point that limit tends to zero. I don't know why. I have seen many proofs on the internet using sandwich theorem, but I just cannot get where am I going wrong..
Please Help me!