- #1
DyslexicHobo
- 251
- 0
Domain and range in ovals--what's this called?
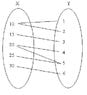
I was helping my friend with his math homework. He's in an intermediate algebra and is working on domains and ranges of functions. He came to me for help with this method of describing domains and ranges of functions using two ovals--one listing the domains of the function and the other the range. I remember learning this in high school, so I was able to help him.
I'm just wondering what this method is called and what it's used for.
Thanks!
I was helping my friend with his math homework. He's in an intermediate algebra and is working on domains and ranges of functions. He came to me for help with this method of describing domains and ranges of functions using two ovals--one listing the domains of the function and the other the range. I remember learning this in high school, so I was able to help him.
I'm just wondering what this method is called and what it's used for.
Thanks!