- #1
Yankel
- 395
- 0
Hello all, I am trying to find and draw the domain of this function:
\[f(x,y)=\sqrt{ln(\frac{9}{x^{2}+y^{2}})}\]
Somehow I find some technical difficulty with it.
I have found 3 conditions:
\[\ln \left ( \frac{9}{x^{2}-y^{2}} \right )\geq 0\]
and
\[\frac{9}{x^2-y^2}>0\]
and
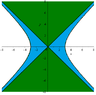
\[x^2\neq y^2\]This led me to understand that maybe an hyperbola is concerned, or a part of it anyway.
I understand that in order to keep
\[\ln \left ( \frac{9}{x^{2}-y^{2}} \right )\geq 0\]
I get
\[\frac{9}{x^2-y^2}\geq 1\]
after applying e. But I am kind of stuck now.
Your help will be most appreciated. I want to draw the domain at the end.
\[f(x,y)=\sqrt{ln(\frac{9}{x^{2}+y^{2}})}\]
Somehow I find some technical difficulty with it.
I have found 3 conditions:
\[\ln \left ( \frac{9}{x^{2}-y^{2}} \right )\geq 0\]
and
\[\frac{9}{x^2-y^2}>0\]
and
\[x^2\neq y^2\]This led me to understand that maybe an hyperbola is concerned, or a part of it anyway.
I understand that in order to keep
\[\ln \left ( \frac{9}{x^{2}-y^{2}} \right )\geq 0\]
I get
\[\frac{9}{x^2-y^2}\geq 1\]
after applying e. But I am kind of stuck now.
Your help will be most appreciated. I want to draw the domain at the end.