I Doppler Analysis of Twin Experiment: Valid Argument?

[Nugatory]

No, it isn't. The stay at home twin's total path length is 250 hours, and the traveling twin's total path length is 150 hours: 75 hours on the outbound leg and 75 hours on the return leg. I computed the 75 hours explicitly in post #24. So the ratio of the proper times is 250 to 150, not 250 to 90.

I was talking about the $1-(v/c)^2$ part…. I have no idea where the 250 and the 90 came from.

 

[PeterDonis]

I was talking about the $1-(v/c)^2$ part….

Which is wrong. The correct ratio of proper times is $\sqrt{1 - (v/c)^2}$. In this case, $v/c = 4/5$, so the ratio of proper times is $\sqrt{1 - (4/5)^2} = 3/5$, or 250 to 150. This is basically the same calculation that I did in post #24, except that I used the corresponding $t$ and $x$ coordinate values for the outbound leg in the stay at home twin's rest frame, which are 125 and 100. That gives a proper time for the traveling twin on the outbound leg of 75. Then the 125 and 75 get doubled to get the values for the entire trip.

I have no idea where the 250 and the 90 came from.

They came from the OP's incorrect belief that the ratio of proper times is $1 - (v/c)^2$, without the square root.

 

[Nugatory]

The correct ratio of proper times is $\sqrt{1 - (v/c)^2}$.

Which is exactly what I said: when he wrote $1-(v/c)^2$ he owed himself a square root.

 

[PeterDonis]

Which is exactly what I said: when he wrote $1-(v/c)^2$ he owed himself a square root.

Ah, sorry, I missed the last part of your post #28.

 

[Dale]

Take a velocity of v=4*c/5 and set the atomic watches on a period of T0= 1 hour, which gives a redshifted period of Tr=3 and a blueshifted period of Tb=1/3. Take a distance of 100 light-hours between the start and the U-turn. The apparent distances covered per period being v*Tr for the outward journey and v*Tb for the return and taking into account the shift of perception of the U-turn discussed above, the traveller counts for the stay-at-home 25 periods during the outward journey and 225 periods during the return journey and the stay-at-home counts for the traveller 45 periods on the outward journey and 45 periods on the return journey. This gives during the entire trip a total duration of 150 hours for the traveler and 150 hours for the stay-at-home. The same.

It is hard to see where you went wrong since you didn't post the derivation, just your final numbers, but this is not entirely correct. Using units where $c=1$ and $v=4/5$ we do have a Doppler redshift factor of 3 and a Doppler blueshift factor of 1/3. Everything below is done in the stay at home twin's frame which is inertial and the coordinates are given as $(t,x)$.

The worldline of the home twin is $$r_{home}=(t,0)$$ while the worldline of the traveling twin is $$r_{twin}=
\begin{cases}
(t,t \ 4/5) & t \le125 \\
(t,200-t \ 4/5) & 125\le t
\end{cases}$$

The worldline of the n-th outgoing (from home to traveling twin) light ray is $$r_{out}=(t,t-n)$$ while the worldline of the m-th ingoing (from traveling to home twin) light ray is $$r_{in}=\begin{cases}
(t,3 \ m-t) & m\le 75 \\
(t,200+m/3-t) & 75 \le m
\end{cases}$$

With $\Delta s^2=-\Delta t^2+\Delta x^2$ and the above worldlines we can confirm that the proper time between each emission and the next is 1, and we can confirm that the proper time between each reception and the next is either 3 or 1/3. So, the Doppler shift formula is correct.

There are a total of 250 emissions from the home twin and a total of 150 emissions from the traveling twin corresponding to a time dilation factor of 5/3, as expected for $v=4/5$. The traveling twin receives 25 signals on the outbound leg (25*3=75) and a total of 225 signals on the inbound leg (225/3=75) so they received redshifted signals for half the trip and blueshifted signals for half the trip. The home twin receives a total of 75 redshifted signals (75*3=225) and a total of 75 blueshifted signals (75/3=25) so they received redshifted signals for most of the trip and blueshifted signals for only the last little bit of the trip.

The times are not equal.

 

[robphy]

Here's a spacetime diagram that displays physically what is going on,
as well as displays every quantity to support the calculations by @Dale and @PeterDonis.
You can count everything and form the necessary ratios,
which will agree with formulas used in various approaches to explain what is going on.

The first diagram shows regular transmissions by the inertial-twin
and how they are received by the non-inertial twin.

The second shows regular transmissions (with same proper period) by the non-inertial twin
and how they are received by the inertial twin.

(Each "diamond" represents 5 hours of proper time.)

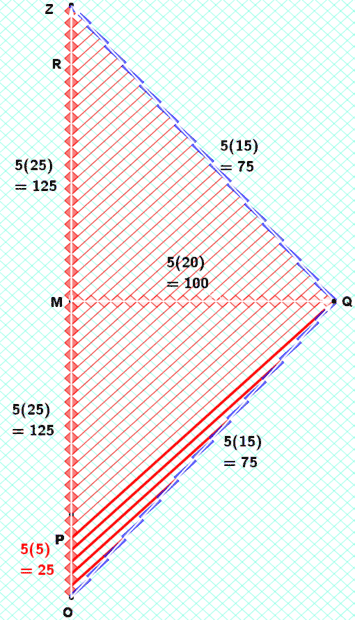
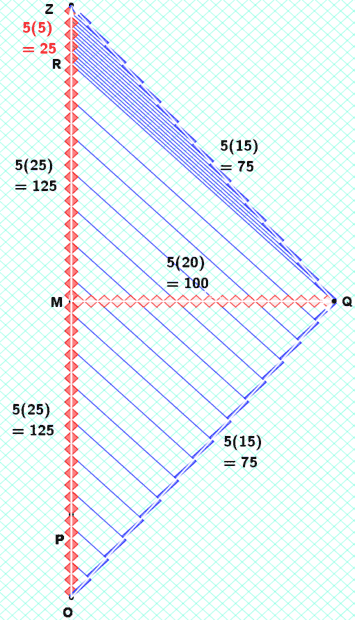
The above uses $v_{separating}=(4/5)c$ and $v_{approaching}=(-4/5)c$.

When separating ,
the ratio of reception-period to transmission-period is $\frac{OQ}{OP}=\frac{75}{25}=3$
using the transmissions by OP,
and
the ratio of reception-period to transmission-period is $\frac{OR}{OQ}=\frac{225}{75}=3$
using the transmissions by OQ. (So, these are lower-frequency receptions.)

When approaching,
the ratio of reception-period to transmission-period is $\frac{QZ}{PZ}=\frac{75}{225}=\frac{1}{3}$
using the transmissions by PZ,
and
the ratio of reception-period to transmission-period is $\frac{RZ}{QZ}=\frac{25}{75}=\frac{1}{3}$
using the transmissions by QZ. (So, these are higher-frequency receptions.)

---

The diamonds are traced out by light-signals in a light-clock.
All diamonds have edges parallel to the rotated graph paper (since the eigenvectors of the boost are along the light cones).
The blue diamonds have the same area as the red diamonds (since the determinant of the boost (the product of the eigenvalues) equals 1).
In fact, the blue diamonds are obtained from the red diamonds
by stretching along one lightlike direction by the Doppler factor $k=3$
and shrinking in the other lightlike direction by the same factor.
The timelike diagonal is along the worldline of the lightclock.
(The spacelike diagonal is simultaneous according to that clock.)

 

[Kairos]

Thanks for all your very helpful remarks! Of course the flashes are by definition emitted every hour in proper times. My above results using only apparent values were supposed to compare the perceived durations, obtained by cross-reading the watches. I completely agree that to switch to proper durations, the number of flashes for the receiver corresponds to the number of hours for the sender. I see my omission of the square root.

 

[robphy]

Possibly entertaining:
@ t=01h10m15s in Einstein’s Universe (Calder)
(the video that got me interested in relativity)

This passage discusses the clock effect with reference to temporal effects with doppler , followed by optical effects associated with doppler.