Albertgauss
Gold Member
- 294
- 37
- TL;DR Summary
- Where would Doppler red shifted objects get perceived within the searchlight (headlight) effect of relativity, in front or behind the relativistic frame?
The images below were taken from the website
https://www.bing.com/videos/rivervi...E198C7F4F9D4EE240C52E198C7F4F9D4EE2&FORM=VIRE
Starting at about min 11:30.
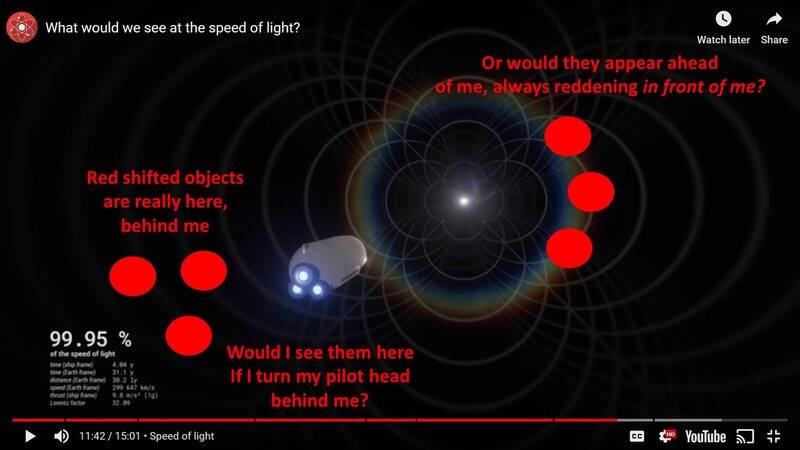
Question: I know that objects that are physically behind me are going to redshift if I look behind me as I travel near light speed. But the searchlight effect is going to compress all of the universe in front of me. So where do I perceive the redshifted objects appear, in front of me or behind me?
My try at an answer: I think I would see the redshifted objects in front of me. I think the searchlight effect would concentrate all the universe in front of me, but within that central cone of vision, some objects really in front would continue to get bluer (since I approach them) but right besides those objects, objects really behind me will get redder, because they are actually receding behind me. That is, within the central cone ahead of me, I will see both bluer and reddening objects right besides each other. Agree or Disagree? My two slides below try to illustrate.

https://www.bing.com/videos/rivervi...E198C7F4F9D4EE240C52E198C7F4F9D4EE2&FORM=VIRE
Starting at about min 11:30.
Question: I know that objects that are physically behind me are going to redshift if I look behind me as I travel near light speed. But the searchlight effect is going to compress all of the universe in front of me. So where do I perceive the redshifted objects appear, in front of me or behind me?
My try at an answer: I think I would see the redshifted objects in front of me. I think the searchlight effect would concentrate all the universe in front of me, but within that central cone of vision, some objects really in front would continue to get bluer (since I approach them) but right besides those objects, objects really behind me will get redder, because they are actually receding behind me. That is, within the central cone ahead of me, I will see both bluer and reddening objects right besides each other. Agree or Disagree? My two slides below try to illustrate.