Double Differentiation and Acceleration in a Four Pulley System

[rudransh verma]

Homework Statement

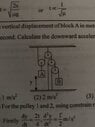
The vertical displacement of block A in meters is $y=\frac{t^2}4$ where t is in sec. Calculate the downward acceleration of block B.

Relevant Equations

$F=ma$

We can differentiate twice the y displacement with respect to time t and get the acceleration of block B. $$a_B= \frac12 m/s^2$$.
But I don’t think it’s that simple.

 

[BvU]

You think correctly
But at least you have the acceleration of A.
How is the position of B in relation to A ? (if A moves up 1 m, how much does B move?)

$\$

 

[rudransh verma]

You think correctly

How is the position of B in relation to A ? (if A moves up 1 m, how much does B move?)

Of course 1 m since all are connected with unstrechable ropes.

 

[BvU]

Your logic is faulty. Think again. Number the pulleys 1,2,3,4 left to right. If 1 goes up by 1 unit, 2 stays in position unchanged, 3 ... etc.

$\$

 

[rudransh verma]

Your logic is faulty. Think again. Number the pulleys 1,2,3,4 left to right. If 1 goes up by 1 unit, 2 stays in position unchanged, 3 ... etc.

$\$

Oh like that!
1 goes up by 1 unit then 2 stays in place, 3 and 4 goes down by 1 unit.

 

[BvU]

2 correct
3 think again, perhaps do the experiment..., or make 2 drawings...

$\$

 

[Lnewqban]

Oh like that!
1 goes up by 1 unit then 2 stays in place, 3 and 4 goes down by 1 unit.

Please, see:
https://www.physicsforums.com/threads/why-is-2dx-dy-in-this-problem.984508/