- #1
HighPhy
- 89
- 8
TL;DR Summary: Analyze, with the help of @Chestermiller, the importance of viscous interactions in a vertical geometry ("Falling ball viscometry") and in an horizontal viscous flow.
The following double experiment was conducted by me a few weeks ago. @Chestermiller and I discussed this experiment privately, and @Chestermiller advised me to open a thread on this Forum so that other users can also benefit from the discussion he and I will have on this topic.
Consider a fluid-dynamic resistance force of intensity ##F## (##\vec F = - \alpha \vec V##) opposing motion at velocity ##V## of a sphere (of radius ##R##, homogeneous, density ##\rho##) inside an incompressible fluid (water, with density ##\rho_W##, contained in a tube of radius ##A \gg R##).1) In the first experiment, the fluid is contained in a tube placed vertically and closed
below, and the sphere is placed inside the tube at various distances below the upper surface of the liquid and left free to move. The sphere left free in the liquid rises to the upper surface; at equilibrium it floats leaving a spherical cap outside the liquid.
I measured the ascent times with a precision of one hundredth of a second (times) as a function of the distance below the surface of the liquid at which the sphere is left (distances). The uncertainty on the distances traveled by the sphere can be considered to be 1 cm. I have reported these values in a table:
$$\small \begin{array}{l|l}
\text{distance (cm)} & \text{time (s)}\\
\hline 100 & 1.77\\
200 & 2.85\\
300 & 3.87\\
400 & 4.86\\
500 & 5.87\\
\end{array}$$
Values are: ##\rho_W = 1.000 \ \mathrm{g/cm^3}##; volume of the sphere ##V_R = 500 \pm 15 \ \mathrm{cm^3}##; volume of the sphere outside water ##V_C = 50 \pm 2 \ \mathrm{cm^3}##
My goal is to calculate (with some relative uncertainty) the viscosity coefficient ##\alpha##. @Chestermiller addressed me to the literature on "Falling ball viscometry".
So, I wrote the equation of motion given by the presence of the buoyancy force, the weight of the sphere, and the viscous resistance ##F = \alpha v##. Noting that the sphere reaches its terminal velocity after a few tenths of a second (the time it takes the sphere to accelerate), I assumed that the acceleration was zero and calculated the velocity as an approximation of the terminal velocity ##v \approx \frac{F_{\text{buoyancy}}-F_{\text{weight}}}{\alpha}##, or alternatively, ##v = \frac{2(\rho_{\text{sphere}}-\rho_{\text{liquid}})r^2 g}{9 \mu}##
But, as @Chestermiller noted, this works only assuming the pipe is horizontal, and that there is no buoyancy. Assuming the pipe is vertical only makes the problem harder. So, we would like to approach the problem from this point of view.
2) Subsequently, I varied the experiment by considering a reserve of the fluid to be contained in a container of cross-section
much greater than that of the tube considered above. The fluid discharges outwards through the tube (therefore, with an L shape) exiting from a circular opening of radius ##a < A## located at a distance ##h## below the level of the fluid in the container. (So, the total thickness of the tube is ##2A## and the total length of the opening is ##2a##).
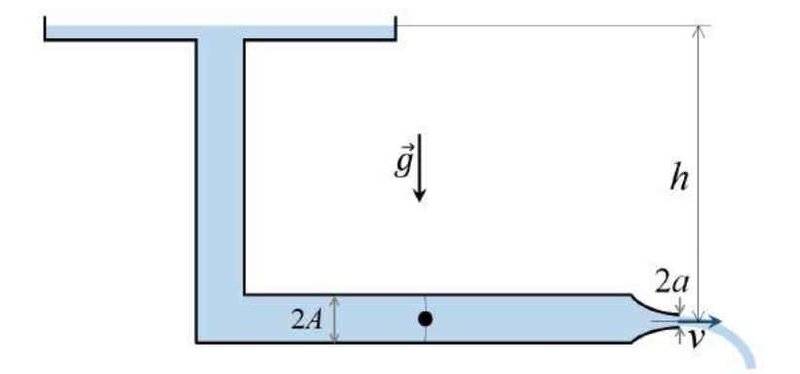
I considered the two hypotheses in which there is or is not the sphere held stationary inside the tube (in the middle). Obviously, there is a difference in velocity in the two cases. In addition to describing the difference from a qualitative point of view, I would like an estimate of the two velocities.
At the very beginning, I calculated the efflux velocity with Bernoulli's law in the case where there is no sphere, and used the continuity equation in the case where there is a sphere, adopting the theorem of mechanical energy and work of non-conservative forces (work of viscous friction) to find the efflux velocity.
But, as @Chestermiller pointed out to me, Bernoulli's equation works only for steady-state inviscid fluids. Admitting the presence of viscous resistance makes the fluid viscous. So, Bernoulli's equation is no longer applicable. It needs to be approached in another way, and @Chestermiller suggested lubrication theory. Besides that, we would like to look at different cases: creeping flow with low Reynolds number, turbulent flow with high Reynolds number, treat Reynolds number as a parameter.
The following double experiment was conducted by me a few weeks ago. @Chestermiller and I discussed this experiment privately, and @Chestermiller advised me to open a thread on this Forum so that other users can also benefit from the discussion he and I will have on this topic.
Consider a fluid-dynamic resistance force of intensity ##F## (##\vec F = - \alpha \vec V##) opposing motion at velocity ##V## of a sphere (of radius ##R##, homogeneous, density ##\rho##) inside an incompressible fluid (water, with density ##\rho_W##, contained in a tube of radius ##A \gg R##).1) In the first experiment, the fluid is contained in a tube placed vertically and closed
below, and the sphere is placed inside the tube at various distances below the upper surface of the liquid and left free to move. The sphere left free in the liquid rises to the upper surface; at equilibrium it floats leaving a spherical cap outside the liquid.
I measured the ascent times with a precision of one hundredth of a second (times) as a function of the distance below the surface of the liquid at which the sphere is left (distances). The uncertainty on the distances traveled by the sphere can be considered to be 1 cm. I have reported these values in a table:
$$\small \begin{array}{l|l}
\text{distance (cm)} & \text{time (s)}\\
\hline 100 & 1.77\\
200 & 2.85\\
300 & 3.87\\
400 & 4.86\\
500 & 5.87\\
\end{array}$$
Values are: ##\rho_W = 1.000 \ \mathrm{g/cm^3}##; volume of the sphere ##V_R = 500 \pm 15 \ \mathrm{cm^3}##; volume of the sphere outside water ##V_C = 50 \pm 2 \ \mathrm{cm^3}##
My goal is to calculate (with some relative uncertainty) the viscosity coefficient ##\alpha##. @Chestermiller addressed me to the literature on "Falling ball viscometry".
So, I wrote the equation of motion given by the presence of the buoyancy force, the weight of the sphere, and the viscous resistance ##F = \alpha v##. Noting that the sphere reaches its terminal velocity after a few tenths of a second (the time it takes the sphere to accelerate), I assumed that the acceleration was zero and calculated the velocity as an approximation of the terminal velocity ##v \approx \frac{F_{\text{buoyancy}}-F_{\text{weight}}}{\alpha}##, or alternatively, ##v = \frac{2(\rho_{\text{sphere}}-\rho_{\text{liquid}})r^2 g}{9 \mu}##
But, as @Chestermiller noted, this works only assuming the pipe is horizontal, and that there is no buoyancy. Assuming the pipe is vertical only makes the problem harder. So, we would like to approach the problem from this point of view.
2) Subsequently, I varied the experiment by considering a reserve of the fluid to be contained in a container of cross-section
much greater than that of the tube considered above. The fluid discharges outwards through the tube (therefore, with an L shape) exiting from a circular opening of radius ##a < A## located at a distance ##h## below the level of the fluid in the container. (So, the total thickness of the tube is ##2A## and the total length of the opening is ##2a##).
I considered the two hypotheses in which there is or is not the sphere held stationary inside the tube (in the middle). Obviously, there is a difference in velocity in the two cases. In addition to describing the difference from a qualitative point of view, I would like an estimate of the two velocities.
At the very beginning, I calculated the efflux velocity with Bernoulli's law in the case where there is no sphere, and used the continuity equation in the case where there is a sphere, adopting the theorem of mechanical energy and work of non-conservative forces (work of viscous friction) to find the efflux velocity.
But, as @Chestermiller pointed out to me, Bernoulli's equation works only for steady-state inviscid fluids. Admitting the presence of viscous resistance makes the fluid viscous. So, Bernoulli's equation is no longer applicable. It needs to be approached in another way, and @Chestermiller suggested lubrication theory. Besides that, we would like to look at different cases: creeping flow with low Reynolds number, turbulent flow with high Reynolds number, treat Reynolds number as a parameter.