Petrus
- 702
- 0
Hello MHB,
I would like to have tips how to solve the x limits for this problem
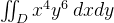 ,
,
there
 Regards,
Regards,
I would like to have tips how to solve the x limits for this problem
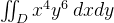
there