Doubt on Morse potential and harmonic oscillator

[Salmone]

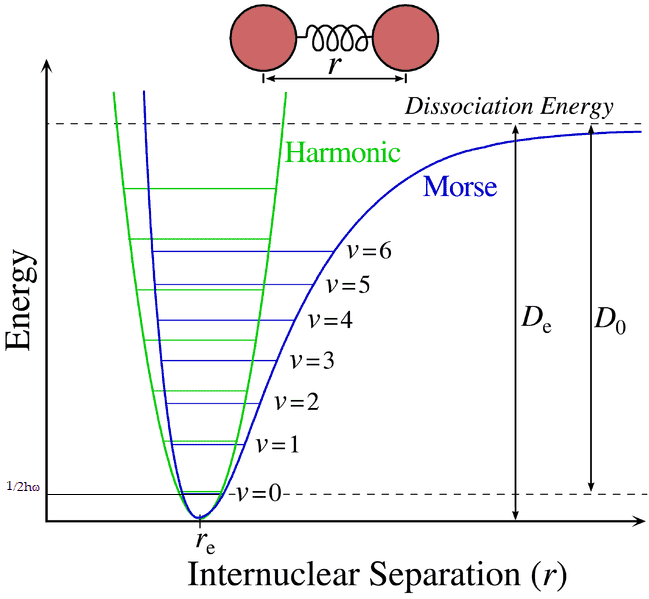
I have a little doubt about Morse potential used for vibration levels of diatomic molecules. With regard to the image below, if the diatomic molecule is in the vibrational ground state, when the oscillation reaches the maximum amplitude for that state the velocity of the molecule must be zero so that the kinetic energy will be zero and the Hamiltonian will be equal to the potential energy for that particular state. Now, since in quantum harmonic oscillator the eigenvalues of the Hamiltonian are equal to $E=\hbar\omega(n+\frac{1}{2})$, for the ground state we have $E=\frac{\hbar\omega}{2}$, so the total energy (kinetic + potential) must be always equal to that value in the G.S., for what I've wrote before then must be that the potential energy corresponding to the orizontal line of the vibrational ground state that is, the potential energy when the maximum amplitude is reached, is equal to $E=\frac{\hbar\omega}{2}$, is it right?

 

[malawi_glenn]

Can you write a shorter question? I have some difficulties understanding what you are really wondering about

 

[Haborix]

I think one issue here is that the OP is mixing quantum and classical mechanics.

Salmone, I agree with the first half of your post as a description of the underlying classical mechanics of a simple harmonic oscillator (I'll ignore the Morse potential, as I think it is irrelevant to the question). However, when you move to quantum mechanics, which you do when you start your discussion of the ground state energy, you have to switch to studying wavefunctions. The danger of combining quantum and classical observations as you have done is that discussion of the kinetic energy and potential energy fails to work in quantum mechanics. In the quantum mechanics of a SHO, the kinetic energy and potential energy do not commute and care has to be taken when you discuss them separately. There are classical-looking states called coherent states, but they are not the ground state, instead they are constructed from a particular sum of all the energy eigenstates.