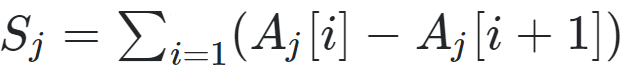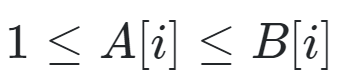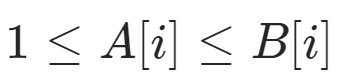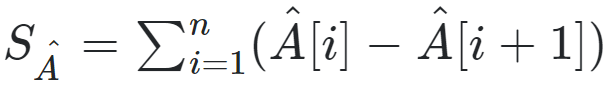DP: proving existence of optimal substructure for "Sherlock and Cost"

[CGandC]

TL;DR Summary

How to prove the existence of optimal substructure for the dynamic programming problem "Sherlock and Cost"?

I was attempting to solve the "Sherlock and Cost" problem from HackerRank using DP:

But before I went to come up with a recursive relation, I wanted to find if the problem possesses an optimal substructure, and I was following these steps as written at CLRS book:

Mentor note: Inline images of mathematical expressions have been replaced by LaTeX.
I did step 1 as follows:
Define $T = \{ \} ~~ . \forall i$ choose $a \in B$ s.t. we define $A = a$ s.t. $1 \le A[ i] \le B[ i]$ . After creating array $A$ perform $T.add(A)$.
Continue adding arrays to set $T$ until all possible added arrays $A$ that satisfy $1 \le A[ i] \le B[ i]$ have been exhausted. Define the set $SUMS = \{ \}$ . Afterwards, $\forall j$ we look at the $jth$ array $A_j \in T$ , define $S_j = \sum_{i = 1} (A_j[ i] - A_j[ i + 1])$ and perform $SUMS.add(S_j)$.
Take $max(SUMS)$ and we're finished. We showed the problem indeed consists of making a choice.Now, I want to prove steps 2+3+4 , this is done by taking an arbitrary object which you wish to optimize and assume that to optimize the object then $X$ will occur, from this assumption subproblems should ensure and you show the solution to each one of them is an optimal solution.
Now, going back to proving steps 2+3+4 in the "Sherlock and Cost" problem, I have no idea what to do, I started with:
" Suppose that in order to find the array $\hat{ A}$ s.t. $S_{ \hat{ A} }$ is $S_{ \hat{ A} } = \sum_{i = 1}({ \hat{ A} }_j[ i] - { \hat{ A} }_j[ i + 1])$ is maximal ... [ stuff to be added ] "
but I have no idea how to continue, how would you proceed to formally proving steps 2+3+4 ( which is proving an optimal substructure exists for the problem )?

Note: Here's an example of how the existence of an optimal substructure is proved for the matrix parenthization problem ( from CLRS chapter 15.2 ) -

Thanks in advance for any help!

 

[Mark44]

Formatting comment -- It looks like you were getting flummoxed by your LaTeX expressions, particularly with the array indexes. In a browser, an expression such as A[i] is interpreted to mean to display A, and then display any subsequent text in italics. A workaround is to insert a space between the left bracket and the index i.

I have replaced most of your attached images, replacing them with Inline LaTeX.

 

[CGandC]

Thanks, I had an issue with displaying array indexes as it seemed to dox my entire text and I couldn't preview correctly before I posted the question ( for some reason, if there are many LaTex expressions the preview won't load them ).

 

[Mark44]

I had an issue with displaying array indexes as it seemed to dox my entire text

Yes. As I mentioned, if you use i for an array index, when it directly follows a left bracket, the browser interprets this to mean "convert all following text to italics." No problem if you use j or k for an array index, or if you insert a space between [ and i. Some other index choices could cause similar problems, such as b (for bold) or u (for underline).

if there are many LaTex expressions the preview won't load them ).

I haven't run into this, except that LaTeX expressions that are very long will cause problems. How long "very long" is I don't know.

 

[sysprog]

Formatting comment -- It looks like you were getting flummoxed by your LaTeX expressions, particularly with the array indexes. In a browser, an expression such as A[i] is interpreted to mean to display A, and then display any subsequent text in italics. A workaround is to insert a space between the left bracket and the index i.

I have replaced most of your attached images, replacing them with Inline LaTeX.

It's not specifically the browser that causes the [i] expression to be interpreted as 'italics on'; it's the bbcode interpreter in the forum software (on PF, that's xenforo) $-$ (I used the ['color=black'] tag between the first bracket and the i to suppress the interpretation of the outer expression as bbcode).

 

[sysprog]

If I type [ i] the space is shown, right? How did you get it it to not be shown, @Mark44?

 

[CGandC]

yes

 

[sysprog]

yes

In post #5 I told of one way to do it; I'm curious as to how @Mark44 did it.

 

[pbuk]

If I type [ i] the space is shown, right?

Not in $\LaTeX : a[ i]$ which is where it was causing the problem. For code, wrap it in [code] or [icode] tags: a[i].

You only need the [color=black]..[/color] hack in plain text.

 

[sysprog]

Not in $\LaTeX : a[ i]$ which is where it was causing the problem. For code, wrap it in [code] or [icode] tags: a[i].

You only need the [color=black]..[/color] hack in plain text.

I see your point, but in post #2, @Mark44 did something that allowed him to show A[i] without it looking like your $\LaTeX$ version.

 

[CGandC]

I managed to concieve of an attempt for proof of the existence of an optimal substructure:

Denote $SEQ$ as the set of all sequences $A$ s.t. $\forall 1 \leq i \leq n$ , $1 \leq A[ i] \leq B[ i]$. For all $A \in SEQ$ define $S_A = \sum_{i=2}^{n}{ | A[ i] - A[ i-1] |}$ .

Let $\hat{A} \in SEQ$ s.t. for every $\hat{A'} \in SEQ$, $S_\hat{A'} \leq S_\hat{A}$.
Thus, there exist a sequence of optimal choices $\langle o_1,o_2,...,o_n \rangle$ s.t. for all $1 \leq i \leq n$ we chose $1 \leq \alpha \leq B[ i]$ s.t. $\alpha \in B$ and we define $\hat{A}[ i] = \alpha$, and this is the $o_i$ choice.
Looking at the sequence of choices $\langle o_1,o_2,...,o_{n-1} \rangle$ and looking at the sequence $\tilde A$ that derives from these choices, $\tilde A$ must be optimal. Otherwise, there exist a sequence of choices $\langle o_1,...,o_l \rangle$ s.t. $l < n-1$ and note that the sequence of choices $\langle o_1,...,o_l, o_n \rangle$ give $\hat{A}$. Notice that we have $l+1$ choices in the sequence $\langle o_1,...,o_l \rangle$ and notice that $\langle o_1,o_2,...,o_n \rangle$ is an optimal sequence of choices, but $l+1 < n$ and since every sequence of choices that yields $\hat{A}$ must have at-least $n$ choices, this means $n \leq l+1 < n$ , a contradiction.

 

[pbuk]

I see your point, but in post #2, @Mark44 did something that allowed him to show A[i] without it looking like your $\LaTeX$ version (n.b.: you can wrap [size] . . . [/size] tags around [icode] . . . [/icode] tags to unshrink the inline code).

If you reply to the message and select 'Toggle BB Code' (the [ ] icon) you can see that he used a variant of the [color=black] hack: A[[COLOR=rgb(0, 0, 0)]i[/COLOR]].

 

[sysprog]

If you reply to the message and select 'Toggle BB Code' (the [ ] icon) you can see that he used a variant of the [color=black] hack: A[[COLOR=rgb(0, 0, 0)]i[/COLOR]].

Yeah, I had forgotten about that $-$ thanks for the reminder.

 

[Jarvis323]

I managed to concieve of an attempt for proof of the existence of an optimal substructure:

Denote $SEQ$ as the set of all sequences $A$ s.t. $\forall 1 \leq i \leq n$ , $1 \leq A[ i] \leq B[ i]$. For all $A \in SEQ$ define $S_A = \sum_{i=2}^{n}{ | A[ i] - A[ i-1] |}$ .

Let $\hat{A} \in SEQ$ s.t. for every $\hat{A'} \in SEQ$, $S_\hat{A'} \leq S_\hat{A}$.
Thus, there exist a sequence of optimal choices $\langle o_1,o_2,...,o_n \rangle$ s.t. for all $1 \leq i \leq n$ we chose $1 \leq \alpha \leq B[ i]$ s.t. $\alpha \in B$ and we define $\hat{A}[ i] = \alpha$, and this is the $o_i$ choice.
Looking at the sequence of choices $\langle o_1,o_2,...,o_{n-1} \rangle$ and looking at the sequence $\tilde A$ that derives from these choices, $\tilde A$ must be optimal. Otherwise, there exist a sequence of choices $\langle o_1,...,o_l \rangle$ s.t. $l < n-1$ and note that the sequence of choices $\langle o_1,...,o_l, o_n \rangle$ give $\hat{A}$. Notice that we have $l+1$ choices in the sequence $\langle o_1,...,o_l \rangle$ and notice that $\langle o_1,o_2,...,o_n \rangle$ is an optimal sequence of choices, but $l+1 < n$ and since every sequence of choices that yields $\hat{A}$ must have at-least $n$ choices, this means $n \leq l+1 < n$ , a contradiction.

I don't quite understand the approach with showing $n \leq l+1 < n$. The logic doesn't quite make sense to me. But I think that the thing you're trying to prove isn't true anyways.

In particular, it isn't true that if $A_{0:n}$ is an optimal solution to the problem of size $n$, then $A_{0:n-1}$ is an optimal solution to the subproblem of size $n-1$.

Here is a counter example,

B = [1, 3, 9]
A = [1, x, 9 ] gives an optimal score which is x-1 + 9 - x = 8, for all valid x.

Meaning the choice of x doesn't matter for deriving the optimal solution, and A = [1,1,9] is optimal.

However, for the sub-problem that choice does matter,

B = [1, 3]
A = [1, x ]

x must be 3 to be optimal (A = [1,1] is not optimal).

Note that this doesn't prove that there is no optimal substructure. I think you will need to define the choices and existence of sub-problems more carefully. E.g. maybe something like using cases, and showing that either this is an optimal sub-problem or that is an optimal sub-problem. Then you can maximize over the choices.

 

[CGandC]

I think you are right because in my proof I don't use any specific property of $S = \sum_{i = 2} |A[ i] - A[ i - 1]|$
and I also think that it's not entirely clear what the subproblems are and how they are used to create a solution to the main problem.
By the way, how could one define the subproblems? and how are they used to create a solution to the larger problem?

 

[pbuk]

From a brief inspection of the problem and the way the value function compares each element of a candidate solution with its predecessor I do not see that it is possible to define independent subproblems: whenever you break before $A_j$ you are not including $A_j - A_{j - 1}$ anywhere.

 

[pbuk]

How could one define the subproblems? and how are they used to create a solution to the larger problem?

Perhaps you should have started with this: there is not much point trying to prove that something is optimal if you have no idea what that something looks like.

 

[CGandC]

From a brief inspection of the problem and the way the value function compares each element of a candidate solution with its predecessor I do not see that it is possible to define independent subproblems: whenever you break before $A_j$ you are not including $A_j - A_{j - 1}$ anywhere.

Like Jarvis above said, I'd have to find another way to define the subproblems because the way I've defined them does not allow the creation of a solution to a larger subproblem. In general, the definitions of subproblems are not unique thus we could define the subproblems in many ways but it can be a very difficult task.

Perhaps you should have started with this: there is not much point trying to prove that something is optimal if you have no idea what that something looks like.

I don't fully agree, sometimes when you are not sure about the trueness of a theorem then attempting to prove it might give you more insight.

One might ask: since the number of subproblems is not necessarily unique, what is the number of possibilities to define subproblems for a DP problem?
Is it even possible to answer this question?