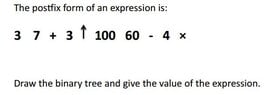MHB Drawing and finding the value of postfix expression

AI Thread Summary
In the discussion about evaluating a postfix expression, it is clarified that ending with no operator means there are two values, 1000 and 160, without a way to combine them. Participants confirm that 1000 and 160 are indeed the final values. The correctness of the drawn Binary Tree is also affirmed. The conversation emphasizes the importance of having an operator to connect values in postfix notation. The conclusion is that without an operator, the final output remains as two separate numbers.
yakin
Messages
42
Reaction score
0
View attachment 2472
View attachment 2473

I am ending with no operator in the end. So 1000 160 would be the answer or what. I do not know what to do from here. Please help!
 

Attachments

  • Capture.JPG
    Capture.JPG
    11.5 KB · Views: 110
  • 20140511_213927.jpg
    20140511_213927.jpg
    53.3 KB · Views: 107
Physics news on Phys.org
yakin said:
https://www.physicsforums.com/attachments/2472
https://www.physicsforums.com/attachments/2473

I am ending with no operator in the end. So 1000 160 would be the answer or what. I do not know what to do from here. Please help!
Yes you end up short one operator, so you have nodes containing 1000 and 160 with no operator to join them.
 
DavidCampen said:
Yes you end up short one operator, so you have nodes containing 1000 and 160 with no operator to join them.
So 1000 and 160 is the answer. And did I draw the Binary Tree right?
 
yakin said:
So 1000 and 160 is the answer. And did I draw the Binary Tree right?

Yes and yes.
 

Thread 'Formal derivation of statement from Peano Arithmetic system'

I was reading a Bachelor thesis on Peano Arithmetic (PA). PA has the following axioms (not including the induction schema): $$\begin{align} & (A1) ~~~~ \forall x \neg (x + 1 = 0) \nonumber \\ & (A2) ~~~~ \forall xy (x + 1 =y + 1 \to x = y) \nonumber \\ & (A3) ~~~~ \forall x (x + 0 = x) \nonumber \\ & (A4) ~~~~ \forall xy (x + (y +1) = (x + y ) + 1) \nonumber \\ & (A5) ~~~~ \forall x (x \cdot 0 = 0) \nonumber \\ & (A6) ~~~~ \forall xy (x \cdot (y + 1) = (x \cdot y) + x) \nonumber...
View full post »

Similar threads

I Can you calculate the probability of a complex logic expression?
Replies
3
Views
2K
B Baccarat math and beating the edge
Replies
1
Views
1K
I Proper understanding of p-value
Replies
5
Views
2K
I Irish lottery record 54-draw rollover, new legislation....
Replies
25
Views
2K
MHB Draw a NAND-gate to get that output
Replies
16
Views
2K
A Confused about magnitude of error
Replies
18
Views
3K
I Does Returning Marbles After Each Draw Affect Chi-square Test Results?
Replies
8
Views
2K
A Low value standard deviation bias
Replies
6
Views
2K
B Odds of Drawing Sequence 4457: Calculating Probability
Replies
8
Views
2K
A Combining model uncertainties with analytical uncertainties
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top