- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hi! (Smile)
I am looking at the following exercise:
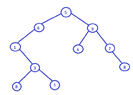
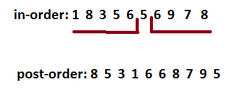
It is given a binary tree with 8 nodes and keys 2,4,6,8,10,12,14,16.The in-order tree traversal gives this order: 2,4,6,8,10,12,14,16.
The pre-order traversal gives the order: 10,8,2,6,4,16,14,12. Draw the tree. Explain how you drawed it.
That's what I have tried:
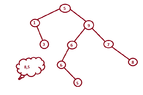
View attachment 3608
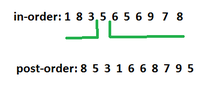
In a pre-order sequence, the leftmost element is the root of the tree.
By searching the root in the in-order sequence, we can find which elements are on the left side of the root, in the left subtree and which are on the right side of the root, in the right subtree. Could you tell me if it is right? (Thinking)
I am looking at the following exercise:
It is given a binary tree with 8 nodes and keys 2,4,6,8,10,12,14,16.The in-order tree traversal gives this order: 2,4,6,8,10,12,14,16.
The pre-order traversal gives the order: 10,8,2,6,4,16,14,12. Draw the tree. Explain how you drawed it.
That's what I have tried:
View attachment 3608
In a pre-order sequence, the leftmost element is the root of the tree.
By searching the root in the in-order sequence, we can find which elements are on the left side of the root, in the left subtree and which are on the right side of the root, in the right subtree. Could you tell me if it is right? (Thinking)