Drawing Geometry Questions: Can You Help?

[ineedhelpnow]

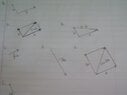
can someone tell me if i drew these right. and also I am stuck on part (f). how do i draw that? i attached the original questions and my drawings.

View attachment 2955

View attachment 2954

for part (a) and (e) i used the parallelogram law

 

[ineedhelpnow]

for (b) should my b vector be pointing the other direction?

 

[Dethrone]

6a to e is right. B is right, but if you want to know, there's two ways to think about it:

b) $a-b = a+-b$

We can apply what we know about adding vectors tip to tail. That is the easiest way to think about it, and I think most people use that way. However, you can also apply vector subtraction, such as $a-b$, by connecting the vectors tail to tail. The resultant vector's tail will be on the tip of $a$, and point towards (the tip of) $b$. (that is easy to prove). So for B, your resultant vector indeed points from $b$ to $a$, which is correct.

 

[ineedhelpnow]

yes that's how i see it. a+(-b) so should my b in that drawing be point in the opposite direction (-b)?

 

[Dethrone]

yes that's how i see it. a+(-b) so should my b in that drawing be point in the opposite direction (-b)?

It's correct as it is. Although, you can physically redraw the vector $b$ as $-b$ by flipping the vector, and connect it head to tail with vector A. This should produce the same vector as you have drawn above. Alternative, you can draw the whole parallelogram, as the following:
http://upload.wikimedia.org/wikiped...llelogram_law.PNG/220px-Parallelogram_law.PNG

- - - Updated - - -

f) is based on the same principle.
$$2b-a$$
We can rewrite it as $2b+ (-a)$. Now we can draw $b$ twice its length, and flip the vector $a$ in the opposite direction. Now connect them head to tail to draw the resultant vector.

 

[ineedhelpnow]

for part (f) i flipped vector a so now its -a and its connected to the tail of 2b (b twice in length) and for (b) i flipped the vector in the opposite direction so it is now -b and is connected to the tail of a. correct?

 

[Dethrone]

Although I think you are right, you have to specify which part of $-a$ (head or tail) that is connected to the tail of $2b$.

 

[ineedhelpnow]

View attachment 2956

 

[Dethrone]

Those look correct. :D

 

[ineedhelpnow]

Thanks Rido!