Drawing the Graph: Analyzing Solutions and Questions

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

,
The solutions is,

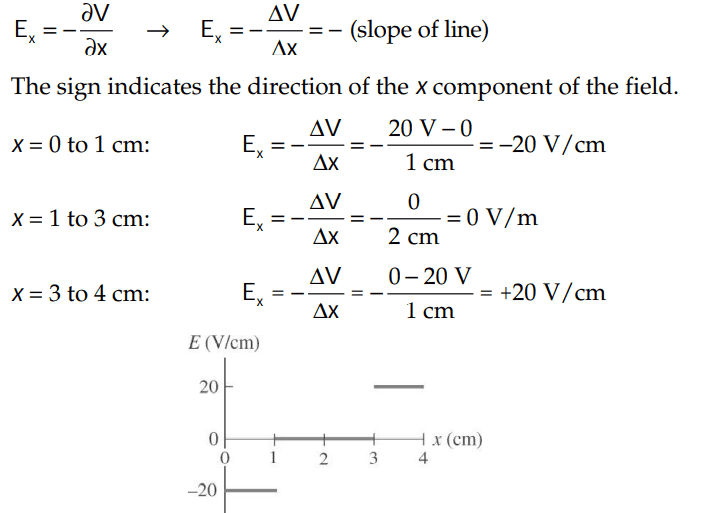
However, why did they not draw vertical lines for the graph like this:

?

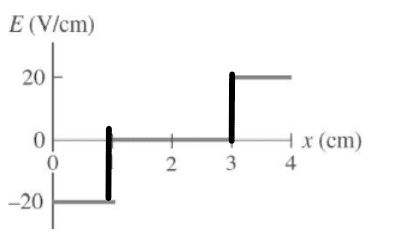Thank you!

 

[kuruman]

However, why did they not draw vertical lines for the graph like this:

Because the electric field is discontinuous at x = 1 cm and x = 3 cm and that is how discontinuous functions are plotted. Drawing a line as you suggest implies that the electric field has all the in-between values which it doesn't.

 

[member 731016]

Because the electric field is discontinuous at x = 1 cm and x = 3 cm and that is how discontinuous functions are plotted. Drawing a line as you suggest implies that the electric field has all the in-between values which it doesn't.

Got it, thank you @kuruman !