Dyadic squares inside of a disc

[Mr Davis 97]

Homework Statement

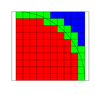
Given $\epsilon$ > 0, show that the unit disc contains finitely many dyadic squares
whose total area exceeds π − $\epsilon$, and which intersect each other only along
their boundaries.

Homework Equations

The Attempt at a Solution

I don't really understand what the problem is asking, especially in terms of the $\epsilon$. If I could get a good grasp of what the problem is asking me to do, perhaps I could solve it.

 

[andrewkirk]

The area of the unit disc is $\pi$, so if the total area of the dyadic squares to exceed $\pi-\epsilon$ then the total area lies in the small open interval $(\pi-\epsilon,\pi)$.

It's asking you to show that, for any tolerance $\epsilon>0$ you can tile most of the inside of the unit disc with dyadic squares, such that all of those squares are entirely within the disc and the area of the disc that is not covered by tiles is less than $\epsilon$. The tiles don't need to all be the same size, but I find it easier to think about when they are.

 

[Mr Davis 97]

The area of the unit disc is $\pi$, so if the total area of the dyadic squares to exceed $\pi-\epsilon$ then the total area lies in the small open interval $(\pi-\epsilon,\pi)$.

It's asking you to show that, for any tolerance $\epsilon>0$ you can tile most of the inside of the unit disc with dyadic squares, such that all of those squares are entirely within the disc and the area of the disc that is not covered by tiles is less than $\epsilon$. The tiles don't need to all be the same size, but I find it easier to think about when they are.

I really can't see how I would get started in showing that. Will it have to do something with Riemann sums?

 

[andrewkirk]

It's a bit like that, in the sense of using very small squares to get as close as desired to the curve.

Here's one approach. Tile the number plane with dyadic squares of side length $2^{-k}$. Now draw a diagram of the boundary region where the disc's curved border intersects squares and you should be able to come up with a formula that gives an upper bound for the total area inside the disc that is not covered by a square that lies entirely within the disc. You should be able to get an upper bound that is a decreasing function of $k$, whose limit as $k\to\infty$ is zero. Then all that's needed is to choose a large enough $k$ so that the left-out area is less than $\epsilon$.

 

[Mr Davis 97]

It's a bit like that, in the sense of using very small squares to get as close as desired to the curve.

Here's one approach. Tile the number plane with dyadic squares of side length $2^{-k}$. Now draw a diagram of the boundary region where the disc's curved border intersects squares and you should be able to come up with a formula that gives an upper bound for the total area inside the disc that is not covered by a square that lies entirely within the disc. You should be able to get an upper bound that is a decreasing function of $k$, whose limit as $k\to\infty$ is zero. Then all that's needed is to choose a large enough $k$ so that the left-out area is less than $\epsilon$.

I am not seeing the connection between diagram and finding a formula. How can I compare squares with a length that depends on k with a circle with an area of $\pi$ that does not depend on k?

 

[andrewkirk]

Draw a small section of the boundary curve, and shade with pencil every square that the curve touches. The untiled area inside the disc must be smaller than the total area of all shaded squares. Can you think of a way of getting an upper bound on the total area of the shaded squares, where the upper bound has limit 0 as $k\to \infty$? Think about the area of a thin annulus that contains the boundary and all shaded squares.

 

[Mr Davis 97]

Draw a small section of the boundary curve, and shade with pencil every square that the curve touches. The untiled area inside the disc must be smaller than the total area of all shaded squares. Can you think of a way of getting an upper bound on the total area of the shaded squares, where the upper bound has limit 0 as $k\to \infty$? Think about the area of a thin annulus that contains the boundary and all shaded squares.

For a square to intersect the circle, wouldn't it have to be through the squares upper-right vertex, since all squares must be contained in the circle? If this is the case then it would seem that many of the squares wouldn't be touching the curve.

 

[Mr Davis 97]

For a square to intersect the circle, wouldn't it have to be through the squares upper-right vertex, since all squares must be contained in the circle? If this is the case then it would seem that many of the squares wouldn't be touching the curve.

Also, would an upper bound for the area of the shaded squares be something like $\displaystyle \pi (\frac{1}{2^{k-1}} + \frac{1}{2^{2k}})$, which comes from the annulus formula?

 

[andrewkirk]

Perhaps this diagram will help. The red squares are the ones that are completely inside the disc. The untiled area inside the disc is less than the total area of the green squares. In fact it's equal to the total area of the parts of green squares inside the disc. Can you draw a smaller, concentric circle inside the existing one, such that all green squares are outside that new circle? Can you get a bound for how much smaller the new circle needs to be, and hence an upper bound on the untiled green area? Can you make that bound depend on $k$ so that it goes to zero as $k\to\infty$?

 

[Mr Davis 97]

Perhaps this diagram will help. The red squares are the ones that are completely inside the disc. The untiled area inside the disc is less than the total area of the green squares. In fact it's equal to the total area of the parts of green squares inside the disc. Can you draw a smaller, concentric circle inside the existing one, such that all green squares are outside that new circle? Can you get a bound for how much smaller the new circle needs to be, and hence an upper bound on the untiled green area? Can you make that bound depend on $k$ so that it goes to zero as $k\to\infty$?

If I start another circle at the bottom of the upmost green square, I would think that the green squares lie completely outside of this circle. Then the area between the inner circle and the outer circle is $\displaystyle \pi - \pi(1- \frac{1}{2^{k-1}})^2$? Would this be an upper bound for the untiled area inside the disc?

 

[andrewkirk]

I am not completely confident that it would not touch any green squares, particularly not one which the curve only cuts right near its top-right corner. It looks like it would probably work OK for this value of k, but we need the procedure to work for any value of k.

To be absolutely sure of not running into problems, calculate the greatest possible distance L(k) between any two points in a k-dyadic square, and draw the new circle with a radius that is L(k) less than the existing circle.

Then you'll be able to use a formula like the one you just wrote. It'll be a somewhat bigger annulus, but its area will still go to zero as $k\to\infty$.

 

[Mr Davis 97]

I am not completely confident that it would not touch any green squares, particularly not one which the curve only cuts right near its top-right corner. It looks like it would probably work OK for this value of k, but we need the procedure to work for any value of k.

To be absolutely sure of not running into problems, calculate the greatest possible distance L(k) between any two points in a k-dyadic square, and draw the new circle with a radius that is L(k) less than the existing circle.

Then you'll be able to use a formula like the one you just wrote. It'll be a somewhat bigger annulus, but its area will still go to zero as $k\to\infty$.

So is $\displaystyle L(k) = \frac{1}{2^{2k-1}}$? I just got this from the Pythagorean theorem. So would the upper bound be $\displaystyle \pi - \pi(1- \frac{1}{2^{2k-1}})^2$?

So does this argument show that we can tile the inside of the circle with finitely many dyadic squares so that we can get arbitrary close to $\pi$ given higher and higher values of $k$? I just want to make sure I am understanding the argument right.

 

[andrewkirk]

How did you derive $L(k)=\frac1{s^{2k}-1}$?

 

[Mr Davis 97]

How did you derive $L(k)=\frac1{s^{2k}-1}$?

Well the greatest possible distance between two points on a dyadic square is the hypotenuse right? So that is $\displaystyle \sqrt{(\frac{1}{2^k})^2 + (\frac{1}{2^k})^2} = \frac{\sqrt{2}}{2^k}$... Oh wait, with that thing I wrote before I forgot to take the square root of.

 

[andrewkirk]

Yes, it's the absence of a square root that was worrying me. With that fixed, what you wrote should be fine.

 

[Mr Davis 97]

Yes, it's the absence of a square root that was worrying me. With that fixed, what you wrote should be fine.

Awesome. So I have a few questions. Why was the fact that we're using dyadic squares important? After specifying the side length of the squares that will tile the plane, wouldn't we get the same result? Also, how would this problem be possible if we had to have that the sides of the squares be dyadic squares be disjoint?

 

[andrewkirk]

Why was the fact that we're using dyadic squares important?

It's not - a fact that strikes me as interesting. The claim remains true if we remove the word 'dyadic' from it. Using dyadic squares provides a nice neat framework whereby we can have all squares the same size $2^{-k}$ and then just take limits as $k\to\infty$. But we could have achieved the same result with any squares. We'd just have had to make a few more definitions in order to identify what squares we were talking about.

The result would not be true is the sides of the squares had to be disjoint, as squares could only touch at corners, which would mean that, for big $k$, only about half of any area would be covered by tiles.

 

[Mr Davis 97]

It's not - a fact that strikes me as interesting. The claim remains true if we remove the word 'dyadic' from it. Using dyadic squares provides a nice neat framework whereby we can have all squares the same size $2^{-k}$ and then just take limits as $k\to\infty$. But we could have achieved the same result with any squares. We'd just have had to make a few more definitions in order to identify what squares we were talking about.

The result would not be true is the sides of the squares had to be disjoint, as squares could only touch at corners, which would mean that, for big $k$, only about half of any area would be covered by tiles.

In Pugh though the exercise after this one is to "Show that the assertion remains true if we demand that the dyadic squares are disjoint." However, this exercise is double starred, meaning "very hard."

 

[andrewkirk]

Oh, OK, I think I can see a solution to this along fractal lines with progressively smaller squares. Here the squares used in the tiling are not all the same size:

Consider an untiled dyadic square space of side $2^{-m}$ surrounded by dyadic tiles of the same size. how much of it can we tile without any tiles touching?

Divide it into a 4x4 array of 16 dyadic squares. We can tile put a tile in one of those without touching any already-tiled squares. Thus we have tiled 1/16 of the untiled area of the square. In other words, we've reduced the untiled area from $2^{-2m}$ to $\frac{15}{16}2^{-2m}$, and the remaining untiled area is made up of dyadic squares.

We can repeat that process k times, at each stage applying the process to every untiled square, thereby reducing the untiled proportion of the original square to $\left(\frac{15}{16}\right)^k$. We can make that untiled area as small as we like by choosing $k$ high enough.

Now, to do the whole problem, first do the tiling without the no-shared-edge restriction, so that the untiled area in the disc is $<\epsilon/2$. Say we used blue tiles for that. Then replace as many blue tiles as necessary by yellow tiles, so that no two blue tiles touch. Finally, apply the above process, tiling over yellow tiles with smaller blue tiles in such a way that the total area of yellow showing through is less than $\epsilon/2$. Then, regarding an exposed yellow area as untiled, we have tiled all of the disc except for an area smaller than $\epsilon$.