Dynamic physical model - automobile wheel suspension confusion

[shivajikobardan]

Homework Statement

dynamic physical model

Relevant Equations

spring mass system equation, electric circuit equation

Been a long time I studied physics that had anything to do with mechanics, so I'm now in need of memorizing almost everything. So I am seeking for some guidance here. This is "system simulation/modeling/discrete event system simulation/etc" type of subject.

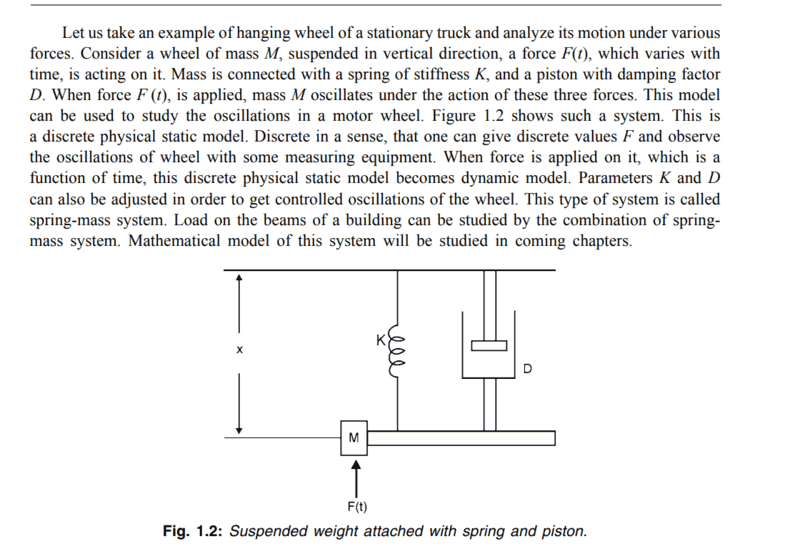
The first thing that I didn't understand is "what point are we trying to make by equating 2 equations" in relation with dynamic physical model?
While i get it that we have analogous equations in real world though.
And I didn't understand how Newton's law of motion was applied to the first figure? And what law is applied in electric circuit in second figure? Coloumb's law? I forgot why are we using derivatives of current L and R but charge q for C?

I know these equations-:

q/C=V

=>V~q

LdI/dt=V
=> V~q**

V=IR
=>V~q*

I guess it is sth like this. But not sure how exactly it was translated (but I think this much information would be enough for this exam for electric circuit part so just help me with physics mechanics part).

 

[BvU]

And I didn't understand how Newton's law of motion was applied to the first figure

Hi,

$F = ma$ is the law applied here. $ma$ appears as $m{d^2x\over dt^2}$ and there are three forces that add up to the $F$. Maybe the fact that they moved over two of them to the other side of the $=$ sign is what confuses you a bit ?

The spring exerts $F_s = -kx$
The dashpot exerts $F_d = - D\dot x = -D {dx\over dt}$
And the exernal force is $F_t$.

The $K$ in front of that in $(1.1)$ is in error. Likewise the ${1\over C}$ in the electric analogon.
(Check the dimensions).

$\$

 

[shivajikobardan]

The $K$ in front of that in $(1.1)$ is in error. Likewise the ${1\over C}$ in the electric analogon.
(Check the dimensions).

$\$

Every other book about this is saying the same thing(written in that book) though.

 

[shivajikobardan]

The dashpot exerts ##F_d = - D\dot x = -D {dx\over dt}

How do you find dashpot force? I didn't get this.

 

[jack action]

Every other book about this is saying the same thing(written in that book) though.

Never seen the spring stiffness associated with the external force before and it doesn't make sense anyway. From Wikipedia:

Deriving the equations of motion for this model is usually done by examining the sum of forces on the mass:

How do you find dashpot force? I didn't get this.

A dashpot, also known as a damper, is a mechanical device that resists motion via viscous friction. The resulting force is proportional to the velocity, but acts in the opposite direction, slowing the motion and absorbing energy.

 

[shivajikobardan]

Never seen the spring stiffness associated with the external force before and it doesn't make sense anyway. From Wikipedia:

yeah not adding it doesn't make any difference.

 

[haider]

Homework Statement:: dynamic physical model
Relevant Equations:: spring mass system equation, electric circuit equation

And what law is applied in electric circuit in second figure? Coloumb's law? I forgot why are we using derivatives of current L and R but charge q for C?

That's Kirchoff's Voltage Law which tells us the sum of potential differences around any closed loop is zero. Applying the law we get
$$E(t) - IR - L\frac{dI}{dt} - \frac{q}{C} = 0$$

You can then rephrase $\frac{dI}{dt}$ and $I$ in terms of the derivatives of charge $q$ . Does that clear your doubt?

Although like BvU said, the $\frac{1}{C}$ on the right has to be an error because the units don't add up. Hope this helped.

 

[shivajikobardan]

That's Kirchoff's Voltage Law which tells us the sum of potential differences around any closed loop is zero. Applying the law we get
$$E(t) - IR - L\frac{dI}{dt} - \frac{q}{C} = 0$$

You can then rephrase $\frac{dI}{dt}$ and $I$ in terms of the derivatives of charge $q$ . Does that clear your doubt?

Although like BvU said, the $\frac{1}{C}$ on the right has to be an error because the units don't add up. Hope this helped.

oh yeah KVL, thanks for the info. this helps for electric circuit doubt.