Dynamic Systems: Calculating Boom Crane's Transfer Motion

[karuthamma]

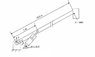
There is boom crane with a bucket attached at the end. The angle of the boom "theta" is 60 degree. The weight of the bucket with a man in it is 200Kg. The mass of the boom is acting at centre of the boom (length of the boom is 10m) is 600 Kg.

There is a cylinder attached to lift the boom 1m from the boom hinge. The hinge of the cylinder is (0.5, -0.3) with respect to the boom hinge (0,0).

Stiffness of the boom modeled by a rotational spring attached at boom hinge is 3x10^5 Nm/rad.

The Cylinder modeled as spring (K= 4x10^6 Nm)and a damper

Assume, 1degree freedom for the oscillation of the crane.

(i)Find Diff. eqn. using Newtons 2nd law of rotational motion at boom's hinge
(ii)Crane natural frequency
(iii)Derive the transfer motion for angular motion as function of wind force F (F=500N, constant & normal to the boom)

I HAVE DONE MY CAL. BUT PLEASE HELP ME IN GUIDING THE APPROACH.

 

[Topher925]

It might help if you actually posted the work you have done. Otherwise we're not going to know your approach or how to help you.

 

[karuthamma]

Thank you for your reply.

Here is the diagram and my work for your ref.

Thanx

 

[karuthamma]

Hello,

Please answer me.

Thanx

 

[Dr.D]

I realize that the problem statement said to use Newton's Second law to formulate the system equation, and in principle that should be sufficient. That does not always make it the easiest way to work the problem, however, and in this case I don't thing it is. The thing that makes this problem more difficult is the manner in which the hydraulic cylinder enters into the situation, and the fact that the cylinder loads act at such a strange angle to the rest of the system.

I worked through the formulation using an energy method called Eksergian's Method (you could also use the Lagrange equation to get the same result). The benefit of doing that is that it forces you to focus first on the kinematics of the problem, and in particular of the cylinder, and then deal later with the kinetics.

What I found is that the system is actually somewhat nonlinear, with a term proportional to the square of the vibratory displacement, and that would be hard to put together from a Newton's Law perspective (at least I think it would), but it falls out very directly from the energy approach.

Ignoring the squared term in the displacement and the damping term, I got an undamped natural frequency of approximately 5.7 rad/s. Do you have any results to compare to this?