Dynamics- Angular Impulse and Momentum Problem

[CylonToaster]

Homework Statement

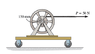
The 30-kg reel is mounted on the 20-kg cart. If the cable wrapped around the inner hub of the reel, with radius 150mm, is subjected to a force of P=50 N, determine the velocity of the cart and the angular velocity of the reel when t=4 sec . The radius of gyration of the reel about its center of mass O is kO = 250 mm. Neglect the size of the small wheels.
Attached is a picture

Homework Equations

I_G*ω₁+Σ \intM_Gdt=I_G*ω₂

The Attempt at a Solution

I=mk²=1.875 kg/m²
So my impulse equation solves down to:
P*r*t=Iω₂+mv₂
I end up with 2 variables and 1 equation. What is my missing equation, or how do I relate ω₂ and v₂?

 

[rude man]

Sorry no one has responded thus far.

Not my specialty, but I would base my computations on two interpretations:

1. Irrespective of the motion of the cart, there is a constant torque τ applied to the reel, with resulting angular acceleration, that torque being τ = P*r1 where r1 = radius of inner hub. Thus θ'' = τ/I and you have already computed I, hopefully correctly.

2. The only force applied to the cart + wheel assembly is P. So P = Mx'' for the assembly where M = total assembly mass (50kg).

If these observations hold then the problem is actually quite straightforward. I think they do. I notice that your "impulse equation" has inconsistent dimensions within it.