Dynamics motion problem with a disk in contact with a bar

[Uchida]

Homework Statement

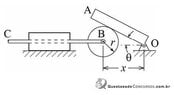
The angular movement of the OA bar, shown in the figure above, is controlled by the horizontal movement of the BC axis, which moves from left to right within the guide. BC velocity is constant and equal to 3 m/s. At the instant shown in the figure, the distance between the center of the disc and the bar joint is x = 2 m. The disk with radius r = 1 m rolls without sliding on the bar OA. With regard to this mechanism, judge the following items:


The OA bar rotates clockwise with an angular speed equal to 30 rpm.

Relevant Equations

Trouble modelling the equations, tried to do with cinematics relations and trigonometrics equations. Got two different (wrong) results.

The answer to the problem is true (ω_OA = 30rpm)

First, I tried to model the disk-bar as a crank connecting rod, to the OA bar, and apply this:

VP = VB + ω_BP x r_P/B, where P is the contact point between the disc and OA bar.

I assumed VP = VP sin 30º i + VP cos 30º j (direction parallel to r_P/B), where r_P/B = sin 30º i + cos 30 j

This gave me:

VP sin 30º i + VP cos 30º j = 3 i - ω_BP cos 30º i + ω_BP sin 30º j.

Solving the linear system, a got VP = 1.5 m/s and ω_BP = 2.6 rad/s = 24.8 rpm.

Considering ω_OA = VP x r_A/O, I got ω_OA = ω_BP.So I tried another aproach:

Considering the x distance in time to be x(t) = 2 - 3t, sin θ(t) = 1/x(t) = 1/(2 - 3t)

Then: θ(t) = sin-¹ [1/(2 - 3t)], and ω_OA = dθ(t)/dt = sqrt(3)/2 rad/s = 8.27 rpm.I am having a lot o trouble solving these cinematics problems involving disk/bar contacts.
I am not able to model mathematically this.

 

[haruspex]

Working with moving contact points is tricky. Can get confused between the motion of that point fixed in the object which happens to be the instantaneous point of contact and motion of the point of contact as an abstract concept.
I could not easily follow your reasoning.

I agree with your result by the second method. It cannot possibly be 30rpm since the conversion from radians brings in a factor $\pi$, and there is no basis for a compensating (inverse) such factor before the conversion.

 

[Uchida]

Working with moving contact points is tricky. Can get confused between the motion of that point fixed in the object which happens to be the instantaneous point of contact and motion of the point of contact as an abstract concept.
I could not easily follow your reasoning.

I agree with your result by the second method. It cannot possibly be 30rpm since the conversion from radians brings in a factor $\pi$, and there is no basis for a compensating (inverse) such factor before the conversion.

Indeed, it is very confusing, and I am not able to model these problems right now.
I am using Hibblers Book, Engineering Mechanics: Dynamics as reference for study. There is some problems like this, but no solved examples (or at least I haven't found them yet).

Those with just bars are ok for me.

Can you recommend me some references about these kind of problems?

I also think that my second approach is correct. It makes sense mathematically. The answer key to the question must be wrong.
However, it is not the method I should be using to get the answer. I must use cinematics equations, since it is the subject I am studying.

 

[Steve4Physics]

For information, I too agree with the 2nd method.

Note: On the diagram, O is shown lower than B and ‘x’ is marked as a horizontal distance. To solve the problem you need to assume the diagram is incorrect - O should be the same height as B.

One approach to this question (and similar ones) is to treat it as a calculus ‘related-rates’ problem:

$sinθ = \frac r x$
We want $\frac {dθ}{dt}$.
$\frac {dθ}{dt}= \frac {dθ}{dx} \frac {dx}{dt}$ (chain rule)

And also, 'cinematics' should be 'kinematics'!

 

[Steve4Physics]

For information, I too agree with the 2nd method.

Note: On the diagram, O is shown lower than B and ‘x’ is marked as a horizontal distance. To solve the problem you need to assume the diagram is incorrect - O should be the same height as B.

One approach to this question (and similar ones) is to treat it as a calculus ‘related-rates’ problem:

$sinθ = \frac r x$
We want $\frac {dθ}{dt}$.
$\frac {dθ}{dt}= \frac {dθ}{dx} \frac {dx}{dt}$ (chain rule)

And also, 'cinematics' should be 'kinematics'!

 

[Uchida]

Note: On the diagram, O is shown lower than B and ‘x’ is marked as a horizontal distance. To solve the problem you need to assume the diagram is incorrect - O should be the same height as B.

Yes, the question is very poorly formulated.

And also, 'cinematics' should be 'kinematics'!

Right!
I need to practice English as well as kinematics!

 

[TSny]

@Uchida
Your first approach is correct except for the very last part where you wrote

Considering ω_OA = VP x r_A/O, I got ω_OA = ω_BP.

Note that the vector equation is not dimensionally correct.

 

[Uchida]

@Uchida
Your first approach is correct except for the very last part where you wroteNote that the vector equation is not dimensionally correct.

Yes! I see! Thank you!

I wrote ω= vr. This is not Correct. It should be v = ωr. What a silly mistake!

Therefore, the correct equation would be VP = ω_OA x r_A/O, which give the same result as the second approach. ω_OA = sqrt(3)/2 rad/s.

So, what I assumed was correct after all: whenever we have a bar in contact with a non slipping circular surface, the instant speed of the contact point will be parallel to the radius taken at the contact point, since a line tangent to a circle is always perpendicular to the radius taken at the contact point . (I was having some doubts about it at first glance)

Oh and yes, now I'm definitely sure the answer key to the problem is wrong.

 

[Steve4Physics]

Out of interest (I lead a boring life) I think that the angular velocity of the bar, $\omega_{OA}$, is unaffected by the presence or absence of slippage between bar and disc.

In this particular problem, the path of the contact point (P) will be the same whether or not slippage occurs.

 

[TSny]

Therefore, the correct equation would be VP = ω_OA x r_A/O, which give the same result as the second approach. ω_OA = sqrt(3)/2 rad/s.

OK. It might be better to write r_P/O instead of r_A/O

So, what I assumed was correct after all: whenever we have a bar in contact with a non slipping circular surface, the instant speed of the contact point will be parallel to the radius taken at the contact point

Yes, this is true if the rod is rotating about some fixed point O such that the line connecting O with the instantaneous point of contact of the disk is tangent to the disk. For example, if the axis of rotation of the rod in your problem is moved to the red dot, then the velocity of the point of contact would not be along the radius of the disk (if the thickness of the rod cannot be neglected). The velocity of the point of contact would be perpendicular to the line connecting the red dot to the point of contact.

Here is an exaggerated figure showing V_P ⊥ OP

 

[Uchida]

@Steve4Physics
Indeed, I can see what you have said.
however, even if the disc has no angular speed, mathematical modeling should be done considering a "virtual bar" from the center of the disc to the point of instantaneous contact, which would eventually have angular speed (this angular speed will be present on the equations), is this correct?

@TSny
Thank you!
You made it very clear to understand.

 

[Steve4Physics]

@Steve4Physics
Indeed, I can see what you have said.
however, even if the disc has no angular speed, mathematical modeling should be done considering a "virtual bar" from the center of the disc to the point of instantaneous contact, which would eventually have angular speed, is this correct?

Yes, Doing it that way is OK. But I'd say 'can be done' rather than 'should be done'.

Remember, other approaches are possible, e.g. your 2nd method or the 'related rates' method in Post #5.

It's a case of selecting the method you're happiest with or feel is most appropriate. There is a phrase in English: 'Horses for courses' - look it up if it's unfamiliar!

Of course, if you have time, using 2 different methods provides a good checking system, as you should get the same answer!