- #1
DMBdyn
- 7
- 0
Homework Statement
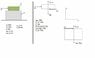
Block B rests upon a smoot surface. If the coefficients of static and kinetic friction between A and B are mu_s=0.4 and mu_k=0.3, respectively, determine the acceleration of each block if P=6lb. (picture attached below)
Homework Equations
Using Newton's Second Law,
[tex]\sum[/tex]Fx=max
[tex]\sum[/tex]Fy=may
The Attempt at a Solution
My free body diagram is in the picture attached below along with values for all variables.
First I sum for the forces in the x-direction.
Because the force of static friction is greater than the force applied to Block A, I assume the force of static friction to reach a value equivalent to the applied force. I take this to mean that Block A is 'stuck', and will not move across the top of Block B.
Newton's 2nd Law applied to Block A:
[tex]\sum[/tex]Fx=mAaxA=P-Ff=6-6=0
Block B is different, as it experiences an equal but opposite force of friction in the positive x-direction. I determine the acceleration of the system from the sum of the forces in the x-direction for Block B (ie. I cannot get a valid answer for the acceleration of Block B using Newton's Second Law unless I assume it's mass to be the sum of both masses).
Newton's 2nd Law applied to Block B:
[tex]\sum[/tex]Fx=(mA+mB)axB=Ff=6
Therefore,
ax,sys=P/(mA+mB)
I'm pretty sure this is correct. However, I'm not sure about my methodology, and I'm also a bit shaky on my conceptual understanding of the problem.
First of all, I'm having a hard time rationalizing the fact that Newton's Second Law tells me Block A experiences no acceleration, when it in fact does experience acceleration. My theory is that my sum of the forces for Block A must be telling me that Block A will not slide over Block B, just as if it were on the ground, it would not slide over the ground. However, Newton's Third Law tells me that there will be an equal and opposite friction force that Block B will experience. At this point, it seems I have two options, 1) Since I know that Block A will not move across Block B, I apply Newton's Second Law to the entire system, or 2) I apply Newton's Second Law to Block B, but substitute the mass of the system for the mass of Block B (using the value of 6 lb for the force of friction, since I have assumed the static force of friction will not exceed the applied force).
Option 1 makes sense to an extent, but Option 2 makes no sense. It doesn't seem to be correct to substitute the mass of the system for the mass of Block B; however, if I don't, I don't think I will get the right answer. Furthermore, option 1 makes sense in that if Block A is not going to move over Block B, then Block B must be moving with Block A, thus I can apply Newton's Second Law to the system to obtain the answer.
Basically, I understand that the top block is not slipping, thus the whole system moves according to Newton's Second Law. However, looking at the free body diagram for the second block yields a phenomenon I cannot explain, since Newton's Second Law has a 6lb force acting on the block, which would give a different acceleration for the bottom block than the acceleration I get for the system.
If clarification is needed just let me know. I'll be glad to accommodate.