Dynamics of Rigid Bodies: The Concept of Law of Gravitation

[Nova_Chr0n0]

Homework Statement

Find the mass of an object (in kg) that weighs 2 kN at a height of 1800 km above the earth’s surface.

Relevant Equations

Mass of earth - 5.9742 x 10^24 kg
Radius of earth = 6378 km
F=G[(m_a*m_b)/R^2]

The questions and relevant formulas/information are attached below:

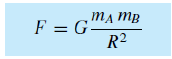
I started by writing the needed values:

2 kN = 2,000 N
6378 km =6378(1000) m
1800 km = 1800(1000)m

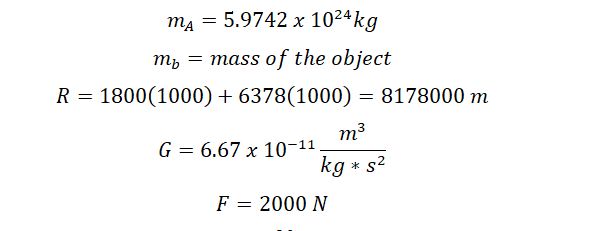
After converting, I tried solving for the mass using the law of gravitation formula:

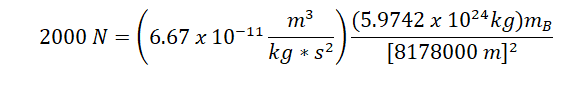
I decided to replace N as (kgm)/s^2:

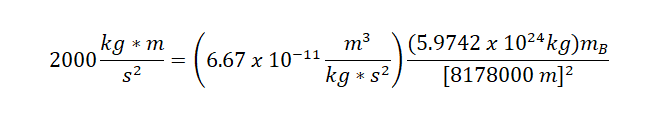
Solving for the mass:

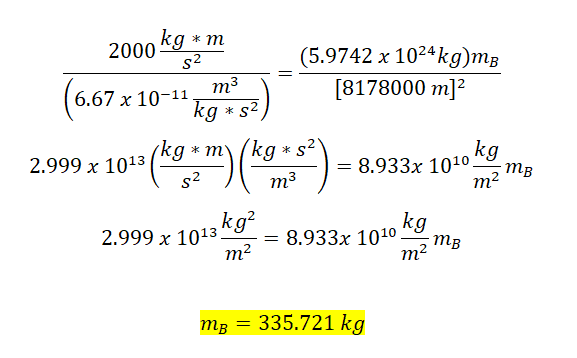
I wanted to verify my final answer by trying to find it in the internet. I only saw 1 solution and we got the same values up until mass B. For his mass B, he got 335.4695 N but I got 335.721 kg. The other solution will be shown below:

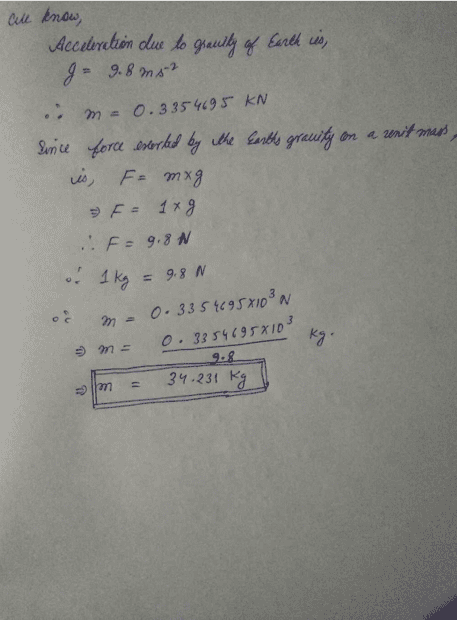
Am I suppose to get mass B here with N as its unit? If so, on what part did I do the algebra wrong?

 

[PeroK]

Mass is measured in kg. Your numerical answer looks correct, although you may think about learning some algebra!