- #1
DaRotot
- 3
- 0
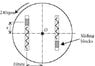
The flat disc rotates around the vertical axis through O a 240rpm (8pi rad/s). each block of 05kg starts of from the spring equilibrium poisition of x = 0.025m. Each spring has stiffness of 400 N/m. Determin the value x and the normal force N of the slot wall on the block. Neglect friction and mass of the springs.
So far I have.
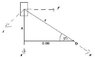
[tex] \sum[/tex]F(t) = 0 = Tsin[tex]\theta[/tex] - Ncos [tex]\theta[/tex]
[tex]\sum[/tex]F(n) = Tcos[tex]\theta[/tex] + Nsin[tex]\theta[/tex] = m.r.[tex]\omega^2[/tex]
[tex]\sum[/tex]F(y) = N = ma(y) = m.a.sin [tex]\theta[/tex]
[tex]\sum[/tex]F(n) = T = k(x -0.025)
r = [tex]\sqrt {0.08^2 + x^2}[/tex]
My brain has pretty much rotted out on this occassion. Thanks
So far I have.
[tex] \sum[/tex]F(t) = 0 = Tsin[tex]\theta[/tex] - Ncos [tex]\theta[/tex]
[tex]\sum[/tex]F(n) = Tcos[tex]\theta[/tex] + Nsin[tex]\theta[/tex] = m.r.[tex]\omega^2[/tex]
[tex]\sum[/tex]F(y) = N = ma(y) = m.a.sin [tex]\theta[/tex]
[tex]\sum[/tex]F(n) = T = k(x -0.025)
r = [tex]\sqrt {0.08^2 + x^2}[/tex]
My brain has pretty much rotted out on this occassion. Thanks
Attachments
Last edited: