E-field for a rectangle of charge

[Xelotath]

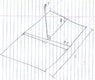
The Problem is finding the E-field at a point P that is h distance from the center of a rectangle (along a line normal to its surface) with Length L and width W with a constant charge density sigma.

This is for an intro E&M class that is supposed to use up through calculus 2, and we have not yet discussed Gausses Law. So supposedly this should be able to be solved without any double or triple integration. Since I have had vector calculus I should be able to understand any help using vector calculus techniques.

Here is what I have tried so far and where I have gotten stuck.

Attached is an image of the problem.
Just in case the image doesn't work, I have set it up so that:

Theta is the angle on the surface between a point along the width at the center and point P.
Phi is the angle on the surface between a point along the length at the center and point P.

I started by saying:
dE=kdqsin(theta)sin(phi)/r^2
But dq=sigmadA and r=sqrt(W^2+L^2+h^2) and sin (theta)=h/sqrt(W^2+h^2) and sin(phi)=h/sqrt(L^2+h^2)
Thus dE=ksigmah^2dwdl/[(L^2+W^2+h^2)sqrt[(h^2+L^2)(W^2+h^2)]]

From this point I have tried lots of algebraic stuff to make it easier to integrate, but I just have not been able to integrate this at all, and I am not sure if it is possible to do so. I am worried that my set up may be wrong. Any help would be much appreciated. Thank you.

 

[tiny-tim]

Welcome to PF!

dE=kdqsin(theta)sin(phi)/r^2
But dq=sigmadA and r=sqrt(W^2+L^2+h^2) and sin (theta)=h/sqrt(W^2+h^2) and sin(phi)=h/sqrt(L^2+h^2)
Thus dE=ksigmah^2dwdl/[(L^2+W^2+h^2)sqrt[(h^2+L^2)(W^2+h^2)]]

Hi Xelotath! Welcome to PF!

(have a square-root: √ and a squared: ² and a theta: θ and a phi: φ )

I'm finding it difficult to read what you've done …

i'm not convinced of the merits of spherical coordinates if the plate isn't a disc …

can I check … you are calculating only the component perpendicular to the rectangle?

 

[Xelotath]

Yes I am using the symmetry argument to say that the resultant E-field is only in the direction normal to the surface of the rectangle at point P, as all the other directions cancel out.

I am not using a spherical reference coordinate system. The sin(theta) and sin(phi) are to find the component of dE in the direction normal to the rectangle.

Sorry about the mess I don't know how to use these forum tools properly yet.
I think I've fixed it here.

dE=$$\frac{kdqsin(\theta)sin(\phi)}{r^{2}}$$

but dq=$$\sigma$$dA and r=$$\sqrt{(W^2+L^2+h^2)}$$ and sin($$\theta$$)=$$\frac{h}{\sqrt{W^2+h^2}}$$ and sin($$\phi$$)=$$\frac{h}{\sqrt{L^2+h^2}}$$

Thus dE=$$\sigma$$$$h^{2}$$kdwdl/[(L^2+W^2+h^2) $$\sqrt{(h^2+L^2)(W^2+h^2)}$$]

Sorry I keep trying to get that last line into a fraction using the tools, but it won't seem to work.

 

[tiny-tim]

I am not using a spherical reference coordinate system. The sin(theta) and sin(phi) are to find the component of dE in the direction normal to the rectangle.
…
dE=$$\frac{kdqsin(\theta)sin(\phi)}{r^{2}}$$

but dq=$$\sigma$$dA and r=$$\sqrt{(W^2+L^2+h^2)}$$ and sin($$\theta$$)=$$\frac{h}{\sqrt{W^2+h^2}}$$ and sin($$\phi$$)=$$\frac{h}{\sqrt{L^2+h^2}}$$

Thus dE=$$\sigma$$$$h^{2}$$kdwdl/[(L^2+W^2+h^2) $$\sqrt{(h^2+L^2)(W^2+h^2)}$$]

Sorry I keep trying to get that last line into a fraction using the tools, but it won't seem to work.

(to do fractions, type \frac{}{} )

ah! that's much easier to read!

surely your cos for the component should just be h/√(h² + w² + l²) ?

 

[Xelotath]

So I have:
E=$$\int\int \frac{k\sigma h}{(L^2+W^2+h^2)^\frac{3}{2}}dwdl$$
after the inner integration with bounds -w/2 to w/2 I get
E=$$\int \frac{2hkw\sigma}{(h^2+L^2)^\frac{3}{2}\sqrt{w^2+4}}dl$$

Thus E=$$\frac{2kwL\sigma}{h\sqrt{(w^2+4)(L^2+h^2}}$$
This still seems wrong
Because by calculations performed myself and seen in my textbook when you take the limit as both W and L approach infinite then E should go to $$2k\sigma$$ but here it is going to $$\frac{2k\sigma}{h}$$
Any ideas? Or can you tell me if I've made some mistake.

 

[tiny-tim]

Hi Xelotath!

E=$$\int \frac{2hkw\sigma}{(h^2+L^2)^\frac{3}{2}\sqrt{w^2+4}}dl$$

No … dimensionally that's wrong …

how did you get it? the obvious thing is to substitute w = √(h² + l²)sinhx or √(h² + l²)tanx.