- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
In summary, the author can't figure out how to do the cosine or sine formulae for a triangle inside a circle. She finds another method using the symmetric lines of the angles and gets the answer of 8.58 cm.
Physics news on Phys.org
- #2
berkeman
Mentor
- 68,306
- 22,033
sponsoredwalk said:The picture speaks for itself, can anyone explain to me how to do this, they put it near the start of my book and i keep coming back to it yet no sine or cosine formulae etc... can help, please :)
Start by drawing more lines on an accurate drawing. Draw a line from where the circle intersects the left line, down to where it intersects the middle of the BC line. Look at the triangle that is formed by that line and the angle B. You know B is 50 degrees, you know the two other angles are equal (to what?). Now look at the corresponding angles inside the circle for a triangle from the center of the circle out to those two points -- what are the angles in that circle? Now can you start filling in some of the distances needed?
- #3
sponsoredwalk
- 533
- 5
(From the book:
I've attached an attempt in picture form, using this logic i continue and use the sine formula but get a wrong result for BC, idk what to do to get 8.58cm.
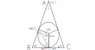
This question comes from chapter 3 and a barely newfound knowledge of sine (soh) and cosine (cah) is expected to explain this. The answer is 8.58cm although i really can't understand how it was accomplished.In the isosceles triangle ABC, the equal angles at B and C are each 50'. The sides of the triangle each touch a circle of radius 2cm.
Calculate the length BC.
I've attached an attempt in picture form, using this logic i continue and use the sine formula but get a wrong result for BC, idk what to do to get 8.58cm.
Attachments
- #4
berkeman
Mentor
- 68,306
- 22,033
sponsoredwalk said:(From the book:
This question comes from chapter 3 and a barely newfound knowledge of sine (soh) and cosine (cah) is expected to explain this. The answer is 8.58cm although i really can't understand how it was accomplished.
I've attached an attempt in picture form, using this logic i continue and use the sine formula but get a wrong result for BC, idk what to do to get 8.58cm.
The angles are labeled wrong. The angles of a triangle add up to 180 degrees. How can one angle be 50 degrees, and the other two angles be 100 degrees apiece?
- #5
berkeman
Mentor
- 68,306
- 22,033
And your drawing does not show a circle in the middle. Is it a circle?
- #6
RTW69
- 374
- 1
Here is another approach. Call the center of the circle O. You know the 2 cm radius of the circle bisects BC. Call that intersection Z. Draw a line from O to C. You now have a triangle OZC. Can you can find the angle OCZ? You know OZ is 2 cm. From the defination of Tangent angle you can find ZC. Twice ZC is BC. It might be helpful to draw a line segment from O to the intersection of the circle and segment AC and indentify all the measures of the interior angles. The answer is indeed 8.58 cm.
- #7
Дьявол
- 365
- 0
Do you know that the intersection of the symmetric lines of the angles create the center of the circle?
I do not find this problem hard to solve.
Here is picture:

just use tan and find BC/2.
Regards.
I do not find this problem hard to solve.
Here is picture:
just use tan and find BC/2.
Regards.
- #8
sponsoredwalk
- 533
- 5
i should have tried it myself, taking tan25'=2/x but i had thought if it and said no to myself, well thanks a lot u've made my day lol :)
FAQ: Easy Trig question that is ridiculously hard
What is "Easy Trig question that is ridiculously hard"?
"Easy Trig question that is ridiculously hard" is a hypothetical trigonometry question that is designed to be difficult and challenging to solve.
Why is it called "Easy Trig question that is ridiculously hard"?
The name "Easy Trig question that is ridiculously hard" is meant to be ironic, as the question is actually quite difficult despite its seemingly simple title.
What makes "Easy Trig question that is ridiculously hard" so difficult?
The question is designed to test your understanding of complex trigonometric concepts and requires a combination of problem-solving skills and mathematical knowledge to solve.
Is there a trick to solving "Easy Trig question that is ridiculously hard"?
There is no specific trick to solving this question, but it may require thinking outside the box and using creative problem-solving methods.
What is the purpose of "Easy Trig question that is ridiculously hard"?
The purpose of this question is to challenge and test your understanding of trigonometry, as well as to improve your problem-solving skills in mathematics.
Similar threads
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 8K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 198
- Views
- 12K
- Replies
- 4
- Views
- 5K
- Replies
- 1
- Views
- 1K
Share: