karush
Gold Member
MHB
- 3,240
- 5
An airplane trip involves three legs, with two stopovers,
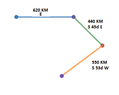
The first leg is due east for 620 km;
the second leg is south- east ($$45^\circ$$) for 440 km
and the third leg is at 53$$^\circ$$ south of west, for 550 km
a. the first thing is to see if there is a way to graph this either with Desmos or someother online grapher
b. What is the plane’s total displacement
ok I know that we need to calculate its magnitude as well as direction for a complete discription.
The first leg is due east for 620 km;
the second leg is south- east ($$45^\circ$$) for 440 km
and the third leg is at 53$$^\circ$$ south of west, for 550 km
a. the first thing is to see if there is a way to graph this either with Desmos or someother online grapher
b. What is the plane’s total displacement
ok I know that we need to calculate its magnitude as well as direction for a complete discription.