EE - Find Unknown Branch Current by Solving Simultaneous Equations

[DaveBoman]

Homework Statement

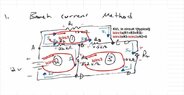
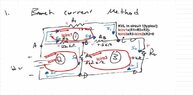
Find branch current by assigning direction arbitrarily and then assigning resistor polarity accordingly. Use KVL around loops and then KCL at nodes to get equations. Solve equations for unknown currents.

Relevant Equations

see picture

 

[DaveBoman]

I am at a complete loss on this problem. I have gotten the loop equations and I have gotten the KCL equations. I have tried to write all of this out thoroughly. I am at a loss as to what to do here.

I have 7 equations and 6 unknowns. The unknowns are I1, I2, I3, I4, IL, and IT, correct?
How can I plug in the KCL equations into the loop equations to get 3 equations and 3 unknowns?

 

[berkeman]

Welcome to PF.

I have 7 equations and 6 unknowns. The unknowns are I1, I2, I3, I4, IL, and IT, correct?
How can I plug in the KCL equations into the loop equations to get 3 equations and 3 unknowns?

I have 3 KCL equations to solve for the 3 node voltages. That is all you need to determine the currents, no?

 

[DaveE]

The KCL equations are linked to the KVL equations by the V-I relationship of each component. So, you actually can create an equation for each component (Like V₁ = I₁⋅R₁), and equation for each node (KCL), and an equation for each loop (KVL). You will have variables for the voltage and current of each component. Of course, as you have seen, you will have way more equations than unknowns. That's OK, use the ones you like, to arrive at a solution for simultaneous linear equations. I will often start by eliminating all of the voltages (in terms of currents), or vice-versa.

You might try it first with a simpler version? In any case if you don't show us what you've done it's hard to help.

 

[vela]

I am at a complete loss on this problem. I have gotten the loop equations and I have gotten the KCL equations. I have tried to write all of this out thoroughly. I am at a loss as to what to do here.

Don't let indecision paralyze you. Sometimes you just need to try something, and you'll see a path forward.

I have 7 equations and 6 unknowns. The unknowns are I1, I2, I3, I4, IL, and IT, correct?
How can I plug in the KCL equations into the loop equations to get 3 equations and 3 unknowns?

Note that the KCL equations aren't independent. The KVL equations and any three of the KCL equations will leave you a system of six equations and six unknowns.

If you want to get down to three equations and three unknowns, just choose three currents to keep in the loop equations. Use the KCL equations to express the other currents in terms of the chosen three.

 

[Babadag]

See [typical]

 

[Babadag]

Wrong KVL