- #1
VinnyCee
- 489
- 0
(a) Using nodal analysis, determine [itex]i_0[/itex] in the circuit.
(b) Now use linearity to find [itex]i_0[/itex].
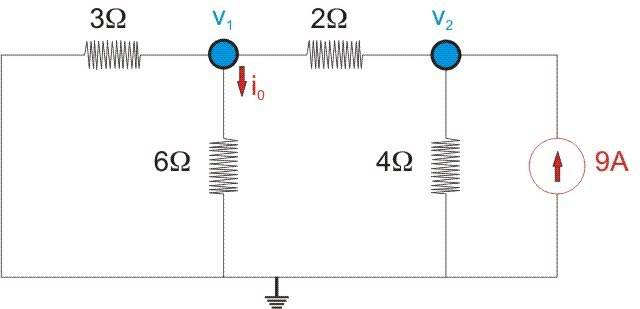
Work so far:
[tex]i_0\,=\,\frac{v_1\,-\,0}{6\,\ohm}\,=\,\frac{v_1}{6\,\ohm}[/tex]
KCL@[itex]v_1[/itex]: [tex]\frac{v_1\,-\,0}{3\,\ohm}\,+\,\frac{v_1\,-\,0}{6\,\ohm}\,+\,\frac{v_1\,-\,v_2}{2\,\ohm}\,=\,0[/tex]
KCL@[itex]v_2[/itex]: [tex]\frac{v_2\,-\,v_1}{2\,\ohm}\,+\,\frac{v_2\,-\,0}{4\,\ohm}\,+\,9A\,=\,0[/tex]
[tex]v_1\,-\,\frac{1}{2}\,v_2\,=\,0[/tex]
[tex]-\,\frac{1}{2}\,v_1\,+\,\frac{3}{4}\,v_2\,=\,-9[/tex]
Whe I put these two equaitons into a 3 X 2 coefficient matrix, I get
[tex]v_1\,=\,-\,9V[/tex]
[tex]v_2\,=\,-\,18V[/tex]
Then I plug into the first equation:
[tex]i_0\,=\,\frac{v_1}{6\,\ohm}\,=\,\frac{(-\,9V)}{6\,\ohm}\,=\,-\,\frac{3}{2}A[/tex]
Is this the correct value for [itex]i_0[/itex] or have I got the sign wrong?
(b) Now use linearity to find [itex]i_0[/itex].
Work so far:
[tex]i_0\,=\,\frac{v_1\,-\,0}{6\,\ohm}\,=\,\frac{v_1}{6\,\ohm}[/tex]
KCL@[itex]v_1[/itex]: [tex]\frac{v_1\,-\,0}{3\,\ohm}\,+\,\frac{v_1\,-\,0}{6\,\ohm}\,+\,\frac{v_1\,-\,v_2}{2\,\ohm}\,=\,0[/tex]
KCL@[itex]v_2[/itex]: [tex]\frac{v_2\,-\,v_1}{2\,\ohm}\,+\,\frac{v_2\,-\,0}{4\,\ohm}\,+\,9A\,=\,0[/tex]
[tex]v_1\,-\,\frac{1}{2}\,v_2\,=\,0[/tex]
[tex]-\,\frac{1}{2}\,v_1\,+\,\frac{3}{4}\,v_2\,=\,-9[/tex]
Whe I put these two equaitons into a 3 X 2 coefficient matrix, I get
[tex]v_1\,=\,-\,9V[/tex]
[tex]v_2\,=\,-\,18V[/tex]
Then I plug into the first equation:
[tex]i_0\,=\,\frac{v_1}{6\,\ohm}\,=\,\frac{(-\,9V)}{6\,\ohm}\,=\,-\,\frac{3}{2}A[/tex]
Is this the correct value for [itex]i_0[/itex] or have I got the sign wrong?