- #1
ItsImpulse
- 26
- 0
Homework Statement
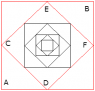
Find the effective resistance across this circuit from two diagonally opposite points on the outer squarehttp://aiminghigh.aimssec.org/wp-content/uploads/2012/01/7squares.gif (I took the image off google it isn't exactly a circuit but its the correct orientation) given that the squares go on to infinity.
Homework Equations
The Attempt at a Solution
I tried to do current analysis which would effectively eliminate the squares in the centre past the second square but upon checking with my teacher, he said that that will not yield the correct answer.
Last edited by a moderator: