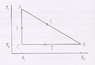
- #1
fluidistic
Gold Member
- 3,949
- 264
Homework Statement
Calculate the efficiency of the heat machine that is shown in the figure. Draw the corresponding Carnot cycle diagram in the S-T plane.
Homework Equations
[itex]\varepsilon = \frac{ \Delta W}{\Delta Q}[/itex].
[itex]\Delta Q = T \Delta S[/itex]
The Attempt at a Solution
My problem lies in evaluating [itex]\Delta Q[/itex] for the process 1 (or from A to B).
For the process 2, [itex]\Delta Q=T_2(S_2-S_1)[/itex].
For the process 3, [itex]\Delta Q=0[/itex] because there's no change in entropy.
But I'm stuck at process 1. My attempt was [itex]\Delta Q=\Delta T \Delta S=(T_2-T_1)(S_2-S_1)[/itex] but I know this doesn't make any sense.
Using that non sensical result I find [itex]\varepsilon = \frac{1}{T_2-\frac{T_2^2}{T_1}}[/itex] which makes no sense because if [itex]T_1=T_2[/itex] I get an infinite efficiency while I should get 0. A friend of mine reached [itex]\varepsilon =\frac{T_1-T_2}{T_1+T_2}[/itex] but I don't know how he did nor if that's right either.
Any help is appreciated.