- #1
patric44
- 308
- 40
- Homework Statement
- the division of two matrices A , B .
- Relevant Equations
- B/A = A^-1 . B = ( 1/delta)(A after changing the sign....) ( B )
he is asking for the division of the two matrices , so i tried to get the inverse of the matrix A but it appears to get more complex as the delta for A is somehow a big equation . and what really bothers me that there is another A , B inside the matrix B ?!
find B/A .
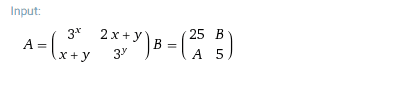
find B/A .
Last edited: