Revisiting Einstein's Train Experiment: Unraveling the Mysteries of Relativity

[GhostLoveScore]

We all know the experiment - here

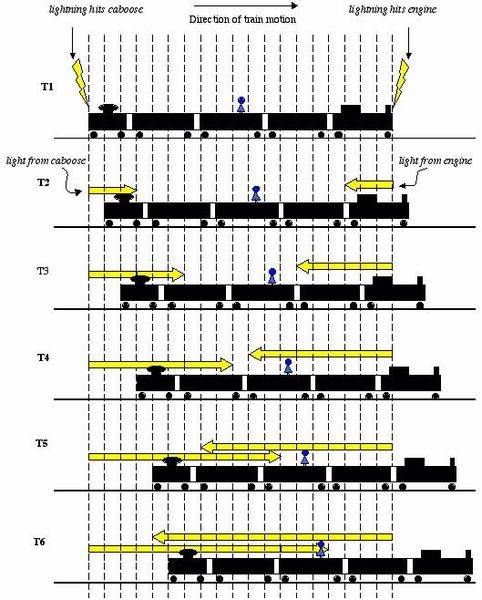
It says that for the observer on a train the lightning strike that we are traveling to happened first, but I have some questions.

1) We are moving towards right, so we must see the right lightning first. And we are moving away from left lightning so that light reaches us later than right lightning light. So that means that if the train speed is 0.5c, than we are moving towards right lightning at 1.5c and moving away from left lightning at 0.5c?

2) So for c to remain constant we say that for the reference frame on the moving train, the right lightning happened first?

That leads me to other question

3) If we were moving with 0.99c towards some galaxy. When we would look at it we would see it accelerated because we were moving towards its light and its time would seem to flow faster?

 

[Orodruin]

First, There is nothing accelerated in the train thought experiment.

Second, you have to distinguish seing something at a certain time and the two things happening at the same time. In the train, these are equivalent because the lightnings are equidistant from the observer.

 

[GhostLoveScore]

That is what I am asking - how do we know that the two lightnings didn't really strike at the same time but we are seeing it in different times because we are at different distances from it? Watching from the moving train reference point.

 

[Orodruin]

Since you know the speed of light and how far away the lightnings are, you can compute when they struck.

 

[GhostLoveScore]

But to me the problem is in understanding this - it seems that for the observer on the train, that we are moving towards right lightning with 1.5c and moving away from left lightning with 0.5c.

 

[Orodruin]

No it does not. You cannot just add velocities in relativity. Light always moves with the speed of light. This is one of the relativity postulates.

 

[GhostLoveScore]

I know. So than the observer on the train would see both lightning flashes at the same time? But it doesn't see both flashes at the same time. See what confuses me?

 

[Orodruin]

I know. So than the observer on the train would see both lightning flashes at the same time? But it doesn't see both flashes at the same time. See what confuses me?

No, I don't know how you could interpret my responses like that. The observer in the train will observe the flashes at different times because in his frame they occur at different times.

 

[GhostLoveScore]

They occur at different times because the light needs time to reach the observer? Is that similar to this - the sun explodes and we see it on Earth. It has happened, but on Mars it is not happened yet since the light didn't react Mars yet?

 

[Orodruin]

They occur at different times because the light needs time to reach the observer?

No. They occur at different times because they occur at different times. It has nothing to do with the actual observation.

 

[GhostLoveScore]

Can you than explain why they occur at different times? And please don't say "because the train is moving".

 

[Orodruin]

Can you than explain why they occur at different times?

Because this follows directly from the postulates of special relativity. In relativity, there is no such thing as an absolute time defining events to be simultaneous, it all depends on the reference frame.

 

[GhostLoveScore]

I think I understand now. An event has happened only when its light reaches us. As I said, any event on the Sun does not happen at the same time for Earth and for Mars, or any other planet?

 

[Orodruin]

An event has happened only when its light reaches us.

No, this makes it obvious that you do not understand.

Whether two events are simultaneous or not in a given frame depends only on how the frame is moving, it has nothing to do with when light is observed.

 

[GhostLoveScore]

OK, more general question - why does the right lightning strike happens first?

 

[A.T.]

OK, more general question - why does the right lightning strike happens first?

This might help:

 

[GhostLoveScore]

But that video also shows that from the ground frame of reference, the photons were fired at the same time, the photon on the right took more time to arrive at the detector because it had to travel longer distance. That doesn't mean that the right photon fired first.

 

[Orodruin]

It seems to me that you are trying to understand relativity simply from reading about the effects and not by looking into how the theory actually predicts these effects. In order to really understand relativity, you need to sit down and read the derivations of the Lorentz transformations, understand how the speed of light being the same in all directions in all frames lead to length contraction and time dilation, and to the relativity of simultaneity.

 

[GhostLoveScore]

Do you have any recommendation on what book to read about that?

 

[Orodruin]

Any textbook on basic special relativity should do. Which one really depends on your level.

 

[A.T.]

But that video also shows that from the ground frame of reference, the photons were fired at the same time, the photon on the right took more time to arrive at the detector because it had to travel longer distance. That doesn't mean that the right photon fired first.

In the video the sending events are simultaneous in both frames, because they are co-located. But the receptions are only simultaneous in one frame, because they are spatially separated. At 1:00 the video explains how this follows from the frame invariant light speed.

For the train, this relativity of simultaneity applies to the sending events, because they are spatially separated here.

 

[GhostLoveScore]

I thought of another question. In moving train frame of reference, if we put a camera with a clock on front and back of a train, and watch the camera recordings later - will the lightning still strike right side (front of the train) first?

 

[Orodruin]

I thought of another question. In moving train frame of reference, if we put a camera with a clock on front and back of a train, and watch the camera recordings later - will the lightning still strike right side (front of the train) first?

Assuming you have synchronised the time stamps on the tapes, yes.

 

[A.T.]

I thought of another question. In moving train frame of reference, if we put a camera with a clock on front and back of a train, and watch the camera recordings later - will the lightning still strike right side (front of the train) first?

Depends on in which frame you synchronized the camera clocks.

 

[GhostLoveScore]

Depends on in which frame you synchronized the camera clocks.

In moving train frame of reference.

 

[A.T.]

In moving train frame of reference.

Then yes.

 

[loislane]

I thought of another question. In moving train frame of reference, if we put a camera with a clock on front and back of a train, and watch the camera recordings later - will the lightning still strike right side (front of the train) first?

The key point as explained by the figure is that the engine and caboose get hit by lightning, on that both the train's and embankment's frames must agree and that there is the same distance to the passenger from the engine and the caboose(in the passenger's frame) . The passenger on the the train observes the light coming from the engine before the light coming from the caboose, while the person at the embankment observes them simultaneously.Thus there is no absolute time. It can be left as an exercise for the reader to determine why an invariant speed c is compatible with traversing equal distances from the train's frame (engine and caboose to passenger) in different times.

 

[15characters]

I know. So than the observer on the train would see both lightning flashes at the same time? But it doesn't see both flashes at the same time. See what confuses me?

I think the confusion here is because you are imagining absolute space. There is no absolute position in space for the light to go off. For example here on Earth we are moving at 30 km every second in orbit around the sun. Imagine an alien hovering next to you at a fixed point in the solar system. If alien stays still in 1 second it will be 30 km away.

Point at something and count to 1. Now remember that the space you were pointing at is now 30 km away.

So if a light flashed on next to you 1 second ago. where is the centre of the expanding circle of light now? next to you or 30 km away?

Imagine if 1 second ago there was an astronaut hovering in a fixed spot in the solar system. And you did a light explosion as you pass this alien, alien will see the light form a perfect circle around him with you speeding away just inside it the circle. Whereas you will see the perfect sphere of light form around you with the alien inside it. Who is right. Who is in the middle of the circle of light?

There is no such thing as an absolute position. Everything is moving.

The appearance of stability on Earth is an illusion

The Earth feels very stable and solid, but it is really like a huge spaceship moving rapidly and smoothly through the solar system.

What I mean is your current location is fixed in relation to earth. Yet the whole thing is moving. So you are traveling through space with a moving frame of reference. So when say 3m in front of me is a specific position in space that is incorrect - for everyone else in the universe not on Earth that point 3m in front of you now is a rapidly moving target.

There is no such thing as an absolute position

This is what is making the train example confusing for you.

You have to drop the idea of an absolute position and remember that the people on the train consider themselves stationary just as you do.

Now bearing this in mind, for the people on the train, they are NOT moving towards the light from the lightning strike. They are stationary and so there is no reason for light to travel faster from the back than the front or vice versa. If they see the light simultaneously from equally distant events, then the events were simultaneous for them.

More complicated example - 3 events

Imagine if Earth had two moons one either side at equal distance (400,000 km). And both lit up at the same time for a brief nanosecond. In our frame of reference these two events were simultaneous. For other frame of reference these two events were not simultaneous.

The third event is the beams of light from each moon hitting Earth simultaneously as detected by a sensor. All observers will agree on this as it is a single event in a single place and time. No observer will deny the sensor on Earth detected both light beams simultaneously.

Now imagine the viewpoint of an alien who sees our solar system rushing past at 99% of the speed of light. He sees the first moon, the Earth and the third moon all speeding past him at 99% of C.

He sees the event of the light beams meeting on earth. He will not deny this occurred. Yet, in his view the location where each moon emitted its light are fixed positions that do not move. He sees the the Earth and moon are moving relative to these fixed positions. In his view the Earth is moving towards the fixed position from when the front moon emitted light and the Earth is moving away from the position where the rear moon emitted its light.

He sees the Earth hit by light from both moons simultaneously, he will assume that the moon that is chasing the Earth's position lit up first. as the light had to travel a greater distance and he will be correct. So the two events are not simultaneous.

Key point to note is that for the alien, the point where the moon emitted the light is a fixed static point on his own reference frame which the moon is moving away from. If you don't appreciate that point you will get confused.
.

 

[GhostLoveScore]

I see, now it's clearer. So in the same situation, train moving to the right - if we have two light bulbs each on one end of the train and we have a switch in the middle of the train where we are. That switch turns on both lights at the same time. What would we see? What would an observer on train station see as we are moving past him?
The difference here is that the light bulbs are moving with the train. The lightning strike was stationary for external observer.

 

[Orodruin]

That switch turns on both lights at the same time.

At the same time in which frame? Just saying "at the same time" does not have any meaning as simultaneity is a relative concept.

 

[GhostLoveScore]

Let's put it this way. Those two light bulbs are blinking. While the train is not moving, they blink at the same time. Then we start moving. What would we see? If I understood this correctly, they would continue to blink at the same time.

 

[Orodruin]

Then we start moving. What would we see?

You are still not specifying the situation properly. You do not mention how the train starts moving. Again, you could specify that the entire train starts moving "at the same time" but this is still ambiguous since you are not specifying which frame you are referring to with your "at the same time". You are also not specifying what you mean by "at the same time" when you state that "they would continue to blink at the same time" - you must specify which frame you are referring to when you make such a statement or the statement will be meaningless.

 

[15characters]

I see, now it's clearer. So in the same situation, train moving to the right - if we have two light bulbs each on one end of the train and we have a switch in the middle of the train where we are. That switch turns on both lights at the same time. What would we see? What would an observer on train station see as we are moving past him?
The difference here is that the light bulbs are moving with the train. The lightning strike was stationary for external observer.

Excellent example. I only just understood how it worked last week. For those on the train and those on the Earth the switching on of the light was an event.

Lets imagine the light bulb in the middle of the train is turned on. For those on the train it is easy to guess what will happen. They are stationary and so is the train. Therefore the light from the light bulb in the middle of the train will hit both end of the train simultaneously.

Now, for you watching from the train track, the train is moving. The back end moves towards the light bulb. The font end moves away from the light bulb. Therefore it is easy to guess what you will see. You will see the light hit the back end first.

How is the phase gap between clocks calculated

Please understand how the difference between the clocks at front and back of train is calculated. It is very simple. Length of train X Relative velocity = time gap.

So the train is 10 light seconds long and moving at 0.5C. What is the gap between front and back clocks?
The Answer is 10 X 0.5 = 5 seconds. It really is that simple to calculate!

If the train was 100 light seconds long and moving at 0.9c what would be the time gap between front an back clocks?

100 x 0.9 = 90 seconds.

Hard question

Moon is 1.25 light seconds away. We have clocks on the moon which we have synchronised with earth.

You fly over Earth towards the moon moving at speed 0.8C. The clock on Earth says the time is 0. What does the clock on the moon say. How many seconds into the future is it?

The answer below

1.25 x 0.8 = 1 second!

Congratulations if you worked it out it is 80% of understanding relativity in my opinion. Learn the invariant equation and you are 100% there. Put it in excel play around converting different times and distances for you and people on the train.

The time gap you see between front and back clocks on a train passing you increases in direct proportion to the proper length of the train and is calculated as length x velocity (for you).

As for your second question, well now you have the formula to see what the time gap between any two clocks on a moving train will be :)

Please note that if you are ON the train the train is NOT moving so there will be no time gap between train clocks.

 

[FactChecker]

Let's put it this way. Those two light bulbs are blinking. While the train is not moving, they blink at the same time. Then we start moving. What would we see? If I understood this correctly, they would continue to blink at the same time.

You have to be more careful when you say "at the same time" for two events that are separated in distance. As @Orodruin has been saying, observers on the train do not agree with stationary observers about "simultaneous" events that occur at a distance. No one person can observe both events since they are separated and moving. Suppose you are on the ground and have carefully synchronized clocks with observers along the tracks. When the light hits the targets, your observers at each target location record the time it hit. They are widely separated but they are using your synchronized clocks. They say that the light hit the back target much earlier than the front target. Suppose people on the train have done the same thing and synchronized their clocks within the train. They record their time at each target location that the light hits both back and front targets. Their recorded times are identical. (In reality, famous experiments came to that conclusion no matter which direction the light was pointed versus the Earth's motion). So you and the train people disagree on what "simultaneous" means for events that are at a distance.

In your example of the light bulbs, the train people would say that the bulbs are always blinking simultaneously. The people on the ground would agree at first, when the train is stationary, but would start to disagree more and more as the train sped up. The rear light would be blinking earlier according to the ground synchronized clocks and the front light would be later.

It's hard to explain why. Experiments kept showing that light traveled at a constant speed in all directions regardless of how fast the person measuring it went in any direction. It's just a fact of physics.

 

[15characters]

Can you than explain why they occur at different times? And please don't say "because the train is moving".

I can follow your thinking cause I was struggling with the same questions a few days ago. Your first question was

"3) If we were moving with 0.99c towards some galaxy. When we would look at it we would see it accelerated because we were moving towards its light and its time would seem to flow faster?"

A) Imagine flying past Earth towards this Galaxy at 99%C. Earth time as you pass is year 0.00

B) The Galaxy is 100 light years away and according to Earth people the time on the Galaxy clock shows year 0.00 at this precise moment Earth clock shows 0.00.

C) You in your ship disagree. Front Clocks run slow by Velocity x Distance. Thus, according to you time on the Galaxy at Earth time = 0.00 is Galaxy time = year 99.00.

(100 light years distance x 0.99c velocity = 99 years of timing phase gap

D For people on Earth your journey to the Galaxy at 0.99c would take 101.01 Earth years. And when you arrive Earth and Galaxy clocks will say 101.01

E) 0.99c produces a gamma factor of 7.09. So for you the distance to the galaxy will be compressed to 14.1 light years and the journey will last 14.2 years.

So:

i) Time on Earth NOW as you pass it is year 0.00. Photons are arriving from the distant Galaxy. They are dated "Galaxy/Earth year -100"

ii) Earth people say the photons now arriving in Earth at speed C from the Galaxy were emitted 100 years ago when the Galaxy clock said year -100. This makes sense to Earth because the Galaxy is always 100 llight years away.

iii) As you fly over Earth at 0.99C the same photon batch labeled "Galaxy/Earth year -100" also hit your rocket ship ...also at speed C. They are pursued by the galaxy rushing in behind yet lagging behind them slightly at a mere 0.99c,

How old are the photons hitting you and the Earth from the Galaxy?

We know the photons from the Galaxy were at one point in time, in the Galaxy. When was this?

If the Galaxy is approaching at 0.99C and the photons at 100%C than they have separated from each other at a speed of 0.01C. At a speed of 0.01 C how long would it take for this photon batch to be 14.1 light away from the galaxy as they are NOW?

14.1 years of distance / speed of 0.01C = time of 1,410 rocket ship years ago.

So 1,410 rocket years X GAMMA is equal to 199.00 Earth years.

Earth says photons are 100 Earth years old we they are 199 Earth years old

Earth says photons arriving now are 100 light years old, and the Galaxy clock must therefore say -100 + 100 = year 0.00

Whereas, we look at the same photons arriving from the galaxy and we say they are ancient and were sent 1,410 rocket ship light years ago when the galaxy was 1,410 light years away by our clocks. We convert the rocket years into Earth years. Earth and the Galaxy clocks run 7 x slower than rocket clocks so 1,410 rocket ship years is 199 Earth years.

What is the current time in the Galaxy based on the photons/images we and Earth are both receiving at Earth time 0.00

Earth says the images it sees from the Galaxy are from 100 light years ago (Earth year -100). We in the rocket say images are from 199 Earth years ago.

So if the images from the Galaxy are from Galaxy clock time -100 years we would expect actual time on the Galaxy NOW to be -100 years plus 199 years. So we say the Galaxy time at Earth time 0.00 is year 99.00

Therefore we and Earth disagree. According to us time now on the Galaxy is year 99.00 . For Earth the time on both Galaxy and Earth clocks is year 0.00.

The difference is 99 years (length x velocity)

So there is a difference of 99 years between what we in our rocket and what those on Earth say the date is NOW in the other Galaxy.

We say what we see NOW is 199 years old and that the Galaxy clock NOW actually shows year 99. Whereas Earth says the images are only 100 light years and so the galaxy clock NOW shows year 0.00.

This is a difference between front and back clocks of 99 years!

Do you know another way to calculate this time difference between Earth and the Galaxy for us.

Distance X Velocity = 99 years!We consider the Galaxy Clock to be 99 Earth years ahead of Earths clock, yet we also claim it is running very slow. How does this work?.

The Galaxy currently at distance of 14.1 light years is moving towards us at 0.99C, It will arrive in 14.2 rocket years. In those 14.2 years the slow Earth / Galaxy clocks will advance by only 2.01 years of Earth / Galaxy time.

When we pass the Galaxy we take a photograph of the Galaxy clock which is synchronised with Earth's clock. What will the Galaxy clocks say at that point?

For Earth

Earth says it is year 0.00 now on the Galaxy. Earth says our trip took 101.01 years. So when we arrive time on Galaxy will be 101.01 years.

For us

Well, according to us Galaxy is at year 99.00 when we pass the Earth clock showing 0.00. Our journey will last 14.2 rocket years. After 14.2 years of our time the slow Galaxy clocks will only move by 2.01 years So when we arrive they will say 101.01 years. So we can take the photo.At the end of the trip

At the end of the trip everyone on the Galaxy both inhabitants and us in our speeding rocket flying past will agree that Galaxy time on our arrival was 101.01. We can take photos.

However, we will disagree on what Earth's clock says at the same moment based on our calculations.

Galaxy inhabitants will say Earth time at our arrival is identical to Galaxy Time 101.01

Rocket people agree Galaxy Time is 101.01 on our arrival. However, we will claim the The Earth Clock simultaneously shows only 2.01. This being 0.00 at our departure plus 2.01 slow Earth years recorded for our trip.

So the time gap of 100 X 0.99C = 99 years remains on arriving in the Galaxy.

Finally

Would we see time accelerate as we approached the galaxy - or rather as it approached us! .

Well, given we are currently looking at an image from minus -199 years ago, and in 14.2 years time we will be looking at the Galaxy at +101.01 years we would see the images updating rapidly.

Yet this would not be fast forward as such - we would be fully aware that we were receiving a barrage of very old images from the Galaxy at high speed due to its approach velocity. It would be like flicking though an album of old photos as you drive to your grand mother's house and just as you arrive you get to the more recent pictures. Time is not accelerated you're looking at the past and flicking through the old images quickly.

We would still conclude that the Galaxy clock advanced by only 2.01 years in a 14.2 year period for us - it would just be that at the start of the journey at Earth time 0.00 we were looking at very old images of the Galaxy from -100 Galaxy years when actually Galaxy time was already simultaneously +99.00;