Electric Circuit. Norton Equivalent current

[Hitman6267]

Electric Circuit. Norton/Thevelin Equivalents

Unsolved Problem

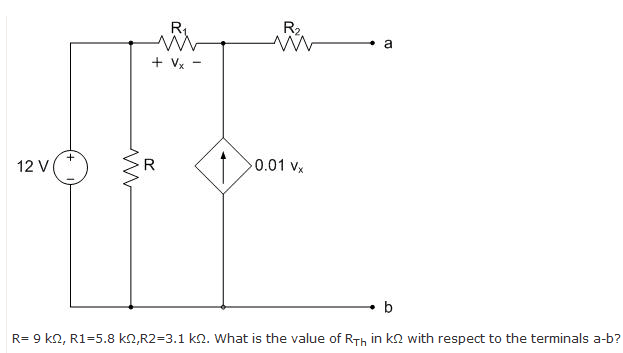
I used a node voltage equation to try and get Vth and the I in the short-circuit to get the Rth but it didn't work.

Unsolved Problem

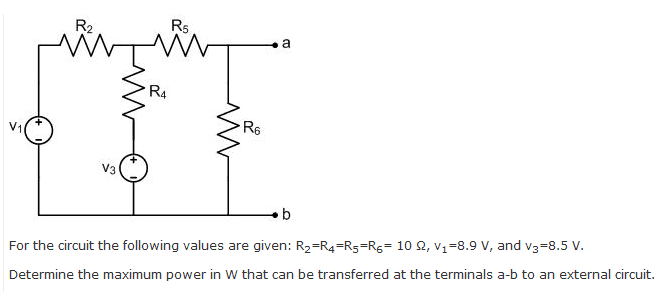
I used a node voltage equation to get Vth and I in the short-circuit. Got Rth and used in the in Vth^2 / 4 RL (with RL = Rth)

My answer was wrong. Is the method correct ?


Solved this my self
Removed to make space for another problem

For me, I find that the Norton equivalent is going to be 12A since the independent current source forces that ampage. But apparently I'm wrong. (I get feedback from a web form when I submit the answer). Any one can tell me what's wrong with my thought process ? Thank you.

Solution:
After doing a source transformation and adding up the resistors. You can get the correct the Norton current value.

Solved

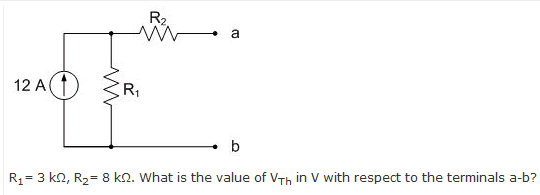
I thought that if I did a source transformation getting a 36000V source would solve the problem because there isn't any other voltage source in the circuit. I was wrong. Any hints on this one ?

 

[vela]

Unsolved Problem
View attachment 24900

I thought that if I did a source transformation getting a 36000V source would solve the problem because there isn't any other voltage source in the circuit. I was wrong. Any hints on this one ?

You're right. The Thevenin voltage is the open-circuit voltage, which is 36000 V.

 

[Hitman6267]

Yes it turns out my answer is correct and that they forgot to ask for the answer in kilo ohm.

Can anyone tell me why the the Vth is equal to the v in the dependent source "3V"

A solution says i = \frac{5-3V}{2000} = \frac{5-3Vth}{2000}

 

[vela]

Think about how you usually determine Vth.

 

[Hitman6267]

I'm going to ask my professor about that problem. Thank you though. Could you have a look at the first problem in my first post ?

I'm pretty sure I need to find Rth using a test source but I can't seem to do it right. (A web form tells me my answer is wrong)

What I tried, I added a current source of 5A to node A. And deactivated the 12V source. The next step for me is to find Vx so I can add it up with R2 * 5A and get Vth. In the end I'll get Rth from, Vth/Ith. But I have failed to get a right answer.Edit: got help with solving it. thank you :)