Electric Circuits: Nodal/Mesh Analysis

[TheCarl]

Homework Statement

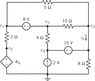
http://edugen.wileyplus.com/edugen/courses/crs4797/dorf1571/dorf1571c04/image_n/n04f090.gif

Determine values of the node voltages, v₁, v₂ v₃, v₄, and v₅ in the circuit shown.

The Attempt at a Solution

Doing nodal analysis I came up with the following four equations but I'm missing one for v5.

(v₁ - v₅)/2Ω + (v₁ - v₃)/5Ω + (v₂ - v₄)/4 = 0

v₂ - v₁ = -8v

v₃/8Ω + (v₃ - v₂)/10Ω + (v₃ - v₁)/5 = 0

v₄ - v₃ = 16

Is there an easy way to find v5 or do I have to attempt mesh current analysis to get v5?

 

[The Electrician]

I don't see any circuit.

 

[TheCarl]

Sorry, must be a login issue. Please see attached.

 

[gneill]

Your first equation seems to be missing a contribution by the current from v2 to v3.

The potential v5 is set by the controlled voltage source. How might you determine $i_x$?

 

[TheCarl]

Yes sorry, I missed that when transcribing it.

(v₁ - v₅)/2Ω + (v₁ - v₃)/5Ω + (v₂ - v₃)/10Ω + (v₂ - v₄)/4Ω = 0

I'm not seeing how I get the i_x without doing a complete mesh current analysis of the circuit. Is that what I have to do?

 

[gneill]

Yes sorry, I missed that when transcribing it.

(v₁ - v₅)/2Ω + (v₁ - v₃)/5Ω + (v₂ - v₃)/10Ω + (v₂ - v₄)/4Ω = 0

I'm not seeing how I get the i_x without doing a complete mesh current analysis of the circuit. Is that what I have to do?

Consider that your node equations are a sum of terms, each of which represents a current between nodes. KCL applied at the right location would seem to be a promising strategy

 

[TheCarl]

So would i_x = (v₃ - v₂)10Ω + (v₃ - v₁)/5Ω ?

 

[gneill]

So would i_x = (v₃ - v₂)10Ω + (v₃ - v₁)/5Ω ?

It would be the negative of that --- consider the directions of the currents that you calculate.

 

[The Electrician]

v₃/8Ω + (v₃ - v₂)/10Ω + (v₃ - v₁)/5 = 0

These 3 currents don't add up to zero unless there is no current in the 16 volt source.

 

[TheCarl]

v3/8Ω + (v3 - v2)/10Ω + (v3 - v1)/5Ω + 16v = 0 ?

Also am I missing something by not incorporating the 2A source in my equations?

 

[gneill]

v3/8Ω + (v3 - v2)/10Ω + (v3 - v1)/5Ω + 16v = 0 ?

Also am I missing something by not incorporating the 2A source in my equations?

Yup. You need to include it in the equation as it pushes current into that supernode. The 16v at the end of the equation doesn't make sense --- 16v is not a current.

 

[TheCarl]

So the actual third equation or the v₃ v₄ supernode would be as follows.

v₃/8Ω + (v₃ - v₂)/10Ω + (v₃ - v₁)/5Ω + v₄/8 + (v₄ - v₂)/4 - 2A = 0

The 16v in the supernode is take care of by the v₄ - v₃ = 16v equation.

Is that correct?

 

[The Electrician]

v3/8Ω + (v3 - v2)/10Ω + (v3 - v1)/5Ω + 16v = 0 ?

Also am I missing something by not incorporating the 2A source in my equations?

When I said "These 3 currents don't add up to zero unless there is no current in the 16 volt source." I didn't mean to just add the quantity "16V" to your equation!

But one end of the 16V is connected to the V3 node and you have to include all the currents into or out of a node. The 16V is connected to things that might provide a current into the left end of the 16V, and that current must also be present at the right end.

Edit: You posted while I was composing my post. It looks like you have got it. Post your final numerical results.

 

[TheCarl]

@The Electrician - Does the new equation that I wrote for the supernode satisfy the currents going in and out of that node or am I still missing something?

 

[The Electrician]

@The Electrician - Does the new equation that I wrote for the supernode satisfy the currents going in and out of that node or am I still missing something?

I think so. I don't see any other paths to the V3 node.

Post your numerical results so I can see how they compare to mine.

What I would typically do in a complicated case like this is to solve in two different ways (typically nodal and mesh) and compare results. I set up for a nodal solution only so far, so if I get the same numbers you do, I'll likely think it's ok.

 

[TheCarl]

See attached for matrix. This is what I got but I think my polarities might be wrong.

v₁ = -8.91v
v₂ = -16.91v
v₃ = -14.63v
v₄ = 1.37v
v₅ = -16.23v

 

[The Electrician]

I'm not getting those numbers. I'll work on this further in a few hours.

 

[The Electrician]

So the actual third equation or the v₃ v₄ supernode would be as follows.

v₃/8Ω + (v₃ - v₂)/10Ω + (v₃ - v₁)/5Ω + v₄/8 + (v₄ - v₂)/4 - 2A = 0

The 16v in the supernode is take care of by the v₄ - v₃ = 16v equation.

Is that correct?

Where did the term in red come from? Leave that term out.

You didn't show your equation for node 5, so I'll just derive it.

The voltage at node 5 is4*((v₂ - v₃)/10Ω + (v₁ - v₃)/5Ω) so your fiifth equation is just a constraint equation:

4*((v₂ - v₃)/10Ω + (v₁ - v₃)/5Ω)=v₅

The numerical result if you make these changes is:

v₁ =11.321v
v₂ = 3.3208v
v₃ = 2.1132v
v₄ = 18.113v
v₅ = 7.8491v

I verified this with Spice. Does this mean I lacked confidence in my result?

This problem was more complicated than the usual ones we see here.

 

[TheCarl]

Hehe thank you so much! You were right on the money. When I had my professor look at my work, he noticed the v4/8ohm error but not the v5 error. Thank you for catching that.

Ya, wasn't that an awesome problem? This is a homework problem in the forth week of intro to circuits. I guess this university believes in baptism by fire.