- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating Electric Field from a Dipole: Is This Equation Accurate?
- Thread starter novelriver
- Start date
In summary, this is the equation for finding the electric field at point p from a dipole. The vector sum of the two electric fields at point P is E = 2kQx/r3.
Physics news on Phys.org
- #2
BvU
Science Advisor
Homework Helper
- 16,110
- 4,870
Hello Novel, 
You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?

You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?
- #3
novelriver
- 7
- 0
BvU said:Hello Novel,
You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?
Thanks for your reply. I'll make sure to not delete the template next time. I think my E describes the magnitude of the electric field. After calculating the magnitude, I can decide if it's positive or negative. So in this case, E is negative, because E is going down, away from positive and toward negative. Is this right?
- #4
BvU
Science Advisor
Homework Helper
- 16,110
- 4,870
I'll give you some leeway because you are new here (let's hope I don't get chastized for that).
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately ). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.
). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.
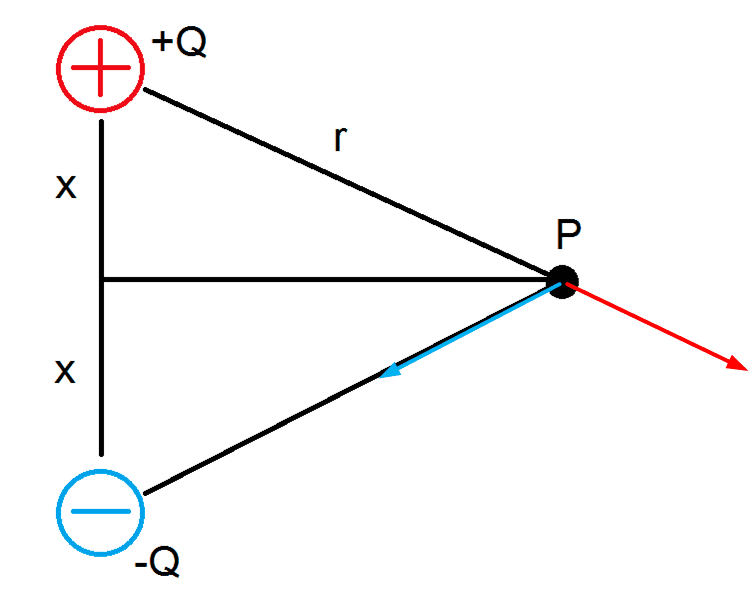
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately
- #5
novelriver
- 7
- 0
BvU said:I'll give you some leeway because you are new here (let's hope I don't get chastized for that).
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.View attachment 105666
I think I understand.
E = kQ/r2 * cos(theta) because the y-components cancel out and we just want to get the x-component. I'll call the horizontal distance d (in a real problem it would be given or I could find it with trig), so cos(theta) = d/r. Therefore E = kQ/r2 * d/r = kQd/r3.
- #6
novelriver
- 7
- 0
novelriver said:I think I understand.
E = kQ/r2 * cos(theta) because the y-components cancel out and we just want to get the x-component. I'll call the horizontal distance d (in a real problem it would be given or I could find it with trig), so cos(theta) = d/r. Therefore E = kQ/r2 * d/r = kQd/r3.
I just realized my mistake. It's the x-components that cancel, not the y. So E = kQ/r2 * sin(theta) = kQ/r2 * x/r = kQx/r3 and then multiply by 2 because there are two charges acting on P in the same direction. So E = 2kQx/r3.
- #7
BvU
Science Advisor
Homework Helper
- 16,110
- 4,870
Looks good to me. x and y are a bit confusing here because of the x's in the figure.
- #8
novelriver
- 7
- 0
BvU said:Looks good to me. x and y are a bit confusing here because of the x's in the figure.
Right, I realized that I should have chose a different variable name than x. Thank you for your help! I appreciate it!
FAQ: Calculating Electric Field from a Dipole: Is This Equation Accurate?
What is an electric field?
An electric field is a region in space where a charged particle experiences a force. It is created by a source charge and can be described as the force per unit charge at a given point in space.
How is an electric field represented?
An electric field can be represented by vector arrows, with the direction of the arrow indicating the direction of the force and the length of the arrow representing the strength of the field.
What is a dipole?
A dipole is a pair of equal and opposite charges that are separated by a small distance. This creates an electric field that is strongest at the ends of the dipole and decreases in strength as you move further away.
How does the distance between charges affect the electric field of a dipole?
The strength of the electric field of a dipole is inversely proportional to the square of the distance between the charges. This means that as the distance between the charges increases, the electric field decreases.
What is the difference between an electric field and a magnetic field?
An electric field is created by stationary charges, while a magnetic field is created by moving charges. Additionally, an electric field can exert a force on a stationary charged particle, while a magnetic field can only exert a force on a moving charged particle.
Similar threads
- Replies
- 11
- Views
- 2K
- Replies
- 14
- Views
- 942
- Replies
- 2
- Views
- 2K
- Replies
- 25
- Views
- 2K
- Replies
- 7
- Views
- 890
- Replies
- 2
- Views
- 349
- Replies
- 19
- Views
- 3K
- Replies
- 1
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 1K
Share:

